人工神经网络与BP算法解析

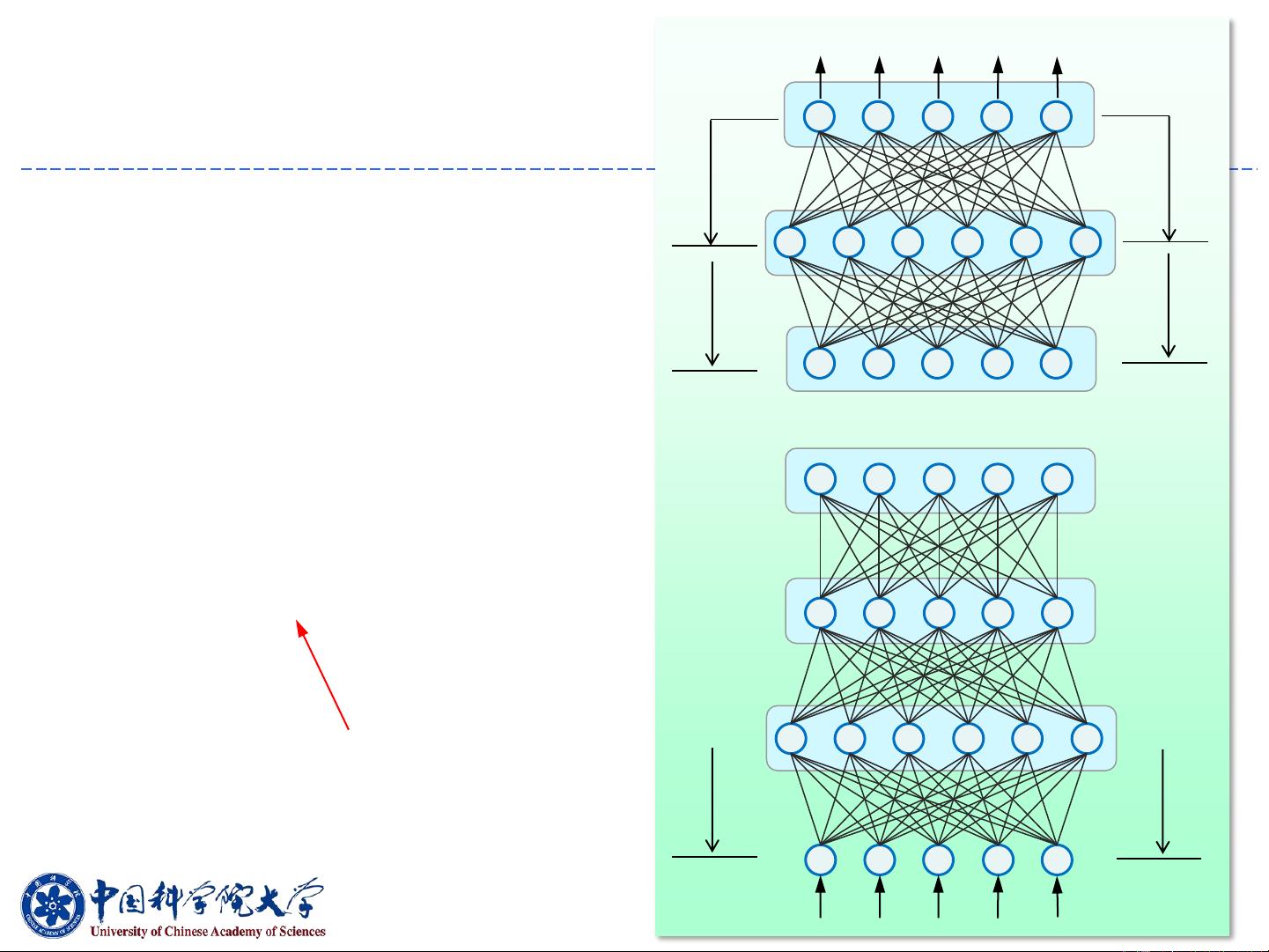
"本次课程是关于人工神经网络的讲解，主要涵盖了神经网络的发展历史、网络结构，以及一些基本和扩展的神经网络模型。此外，还深入讨论了反向传播（BP）算法，包括准则函数的选择，如平方误差准则和交叉熵准则，并介绍了激励函数的重要性，特别是非线性、连续可导和单调性的要求，如Sigmoid和ReLU函数。同时，提到了隐含层数对神经网络性能的影响。" 神经网络是一种模仿人脑神经元结构的计算模型，广泛应用于模式识别、图像处理、自然语言处理等领域。在第8讲中，讲师主要围绕神经网络的基础和扩展模型展开讲解。 首先，神经网络的发展历史被简要介绍，强调了它在人工智能领域的关键地位。接着，课程探讨了神经网络的结构，包括输入层、隐藏层和输出层，以及它们之间的连接权重。 在基本模型部分，单层感知器是最简单的形式，它可以解决线性可分问题；多层感知器通过引入隐藏层，能够解决非线性问题；而径向基函数（RBF）网络利用径向基函数作为激活函数，适用于数据的分类和回归任务。 扩展模型部分涉及了各种先进网络结构，如Hopfield网络用于联想记忆，受限玻尔兹曼机（RBM）用于特征学习，深度神经网络（DNN）通过多层结构提高模型复杂度，卷积神经网络（CNN）在图像识别上表现出色，自动编码器（Autoencoder）用于数据压缩和降噪，循环神经网络（RNN）和长短期记忆网络（LSTM）处理序列数据，如时间序列分析和自然语言理解。 课程中，反向传播（BP）算法作为优化神经网络权重的主要方法被详细讨论。BP算法通过梯度下降法更新权重，以最小化准则函数。在回归问题中，通常采用平方误差准则，而在分类问题中，交叉熵准则更为常见。这两种准则函数都用于衡量网络预测与真实值之间的差异。 激励函数是神经网络的核心组成部分，负责将节点的加权输入转换为输出。Sigmoid函数和双曲正切函数曾是常见的选择，因为它们满足非线性、连续可导和单调性，但因为梯度消失问题，现在更倾向于使用ReLU函数及其变种，如Leaky ReLU和ELU，这些函数在训练过程中能有效减少梯度消失现象，提高模型的训练效率。 最后，课程指出隐含层数的选择对神经网络性能至关重要。适当的隐层数量可以帮助模型捕捉数据的复杂性，同时避免过拟合。更多的隐藏层可以增加模型的表达能力，但也会增加训练的复杂度和可能的过拟合风险。 这堂课全面地介绍了神经网络的基础知识和一些高级主题，为学生提供了深入理解和应用神经网络的坚实基础。