递归算法探秘：从捕鱼问题到斐波那契数列

"这篇资料主要介绍了递归算法的原理及其在解决经典问题中的应用，例如捕鱼问题和运动会金牌问题，并通过实例解释了递归的概念。资料来自天津城市建设学院电子与信息工程系计算机应用教研室的唐国峰教授的课程，其中提到了递归在日常生活中的体现，以及经典的斐波那契数列问题。" 递归算法是一种基于函数或程序自身调用来解决问题的方法，它通过把复杂的问题分解为规模较小的同类问题来逐步求解。在递归过程中，问题的解往往依赖于相同问题的更小规模的解。递归可以被视为一种自我相似的重复，类似于德罗斯特效应，即一个图形或图像在自身内部不断重复。 生活中的递归现象比比皆是，例如在多面镜子的反射中，每一个镜子的映像是前一面镜子的缩小版，形成无穷的反射链。而在算法领域，递归则是直接或间接调用自身的过程，这样的函数称为递归函数。 递归算法的使用通常涉及以下几个关键要素： 1. **基本条件**（Base Case）：这是递归终止的条件，当满足这个条件时，不再进行递归调用，而是直接返回结果。 2. **递归情况**（Recursive Case）：当不满足基本条件时，问题被分解为更小规模的子问题，这些子问题同样通过递归调用来解决。 3. **合并结果**（Combination）：在递归调用结束后，将各个子问题的解组合起来，得到原问题的解。 以描述中的年龄问题为例，第5个人的年龄可以通过递归地计算第4、3、2、1个人的年龄来得出，每次增加2岁。这是一个简单的线性递归问题，通过递归调用可以轻松找到答案。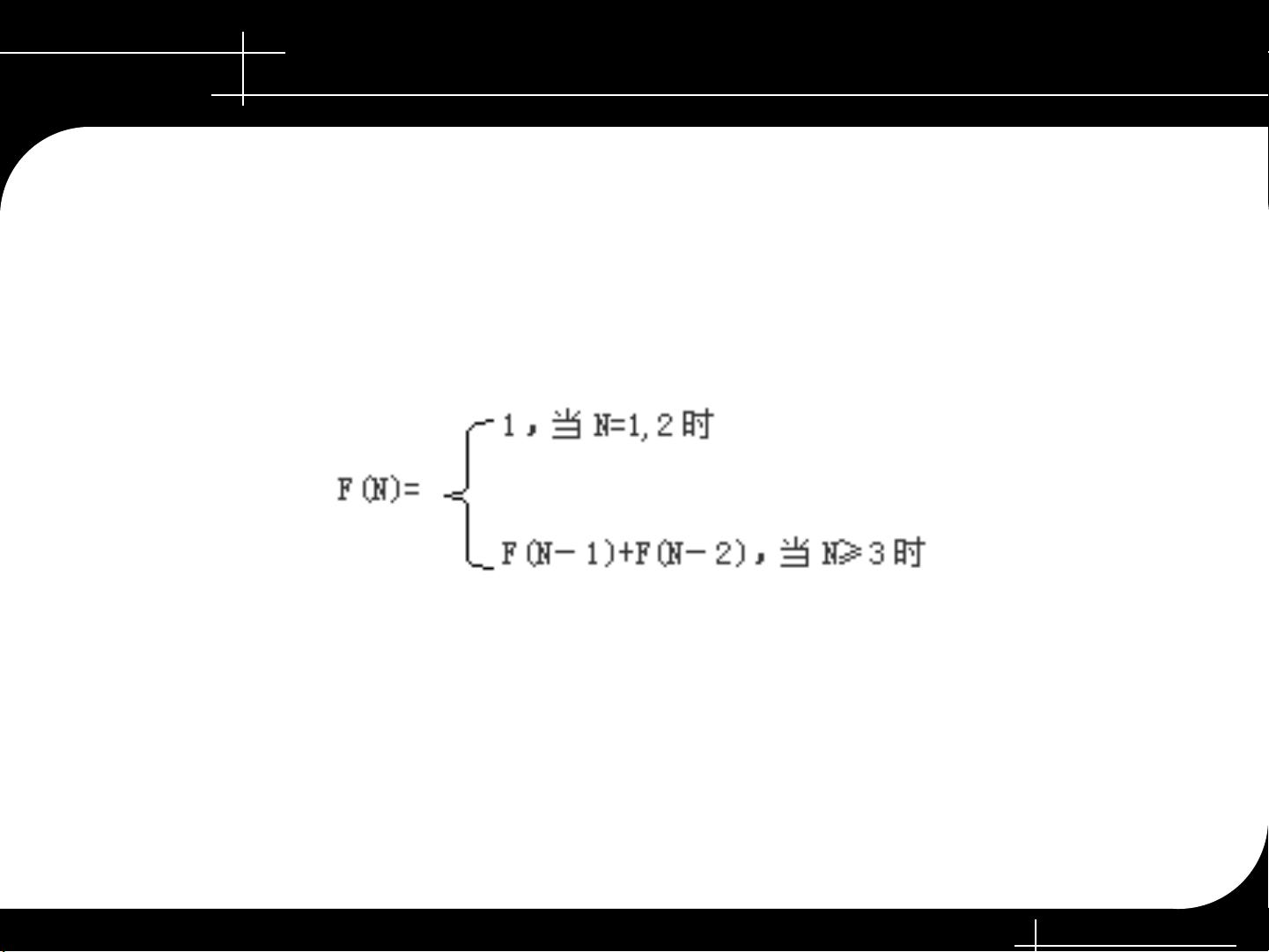 另一个经典的递归问题——斐波那契数列，其特点是每个数是前两个数的和。初始值为F(1)=1，F(2)=1，对于n>2，F(n)=F(n-1)+F(n-2)。斐波那契数列展示了递归算法如何处理数学问题，同时也揭示了自然界中自相似结构的数学模型。 在解决递归问题时，需要注意几个关键点： - **效率**：递归算法可能会导致大量的重复计算，如果不加以优化，可能导致效率低下。 - **栈空间**：每一次函数调用都会占用一定的栈空间，深度递归可能导致栈溢出。 - **正确性**：确保递归的终止条件设置正确，避免无限递归的发生。 在实际编程中，递归算法常常用于解决树形结构、分治策略和动态规划等问题。例如，搜索算法中的深度优先搜索（DFS）、数据结构中的二叉树遍历等。虽然递归有时可能导致复杂性较高，但它的优雅和简洁性使其在解决特定类型问题时具有很大的价值。通过理解递归的基本原理并熟练运用，开发者可以更好地解决那些可以用递归方式表达的问题。