后缀数组：高效字符串处理工具揭秘

后缀数组是字符串处理领域中的一种高效数据结构，由芜湖一中许智磊介绍，它为字符串操作提供了强大的工具。后缀数组的基本概念是通过将一个字符串的所有后缀按字典顺序排序并存储其起始位置来构建的。这个排序过程的结果被存储在一个数组中，称为后缀数组，每个数组元素对应一个后缀的起始位置。 在后缀数组的定义中，首先设定一个字符集Σ，字符串S被假设有n个字符，且以特殊字符"$"结尾，以确保与其他字符区分。后缀是从字符串的某位置i开始直到结尾的部分，例如Suffix(i)表示S[i..len(S)]。字符串间的大小关系是基于字典顺序进行的，通过排序得到的后缀数组SA和相应的名次数组Rank，帮助我们在常数时间内查找后缀在排序列表中的位置。 传统的字符串排序方法效率低下，因为会将后缀看作独立的字符串进行处理，没有考虑到它们之间的内在关联。为此，后缀数组的构造方法引入了倍增算法（DoublingAlgorithm）。这种方法通过逐步增加比较的前缀长度k，使得在2k-前缀意义下比较后缀相当于在k-前缀意义下比较后缀的一部分。这种递归的思想极大地提高了排序效率，将复杂度从O(n^2)降低到了线性时间复杂度O(nlogn)。 具体步骤包括： 1. 将n个后缀视为n个字符串，利用标准排序方法进行初步排序，但效率不高。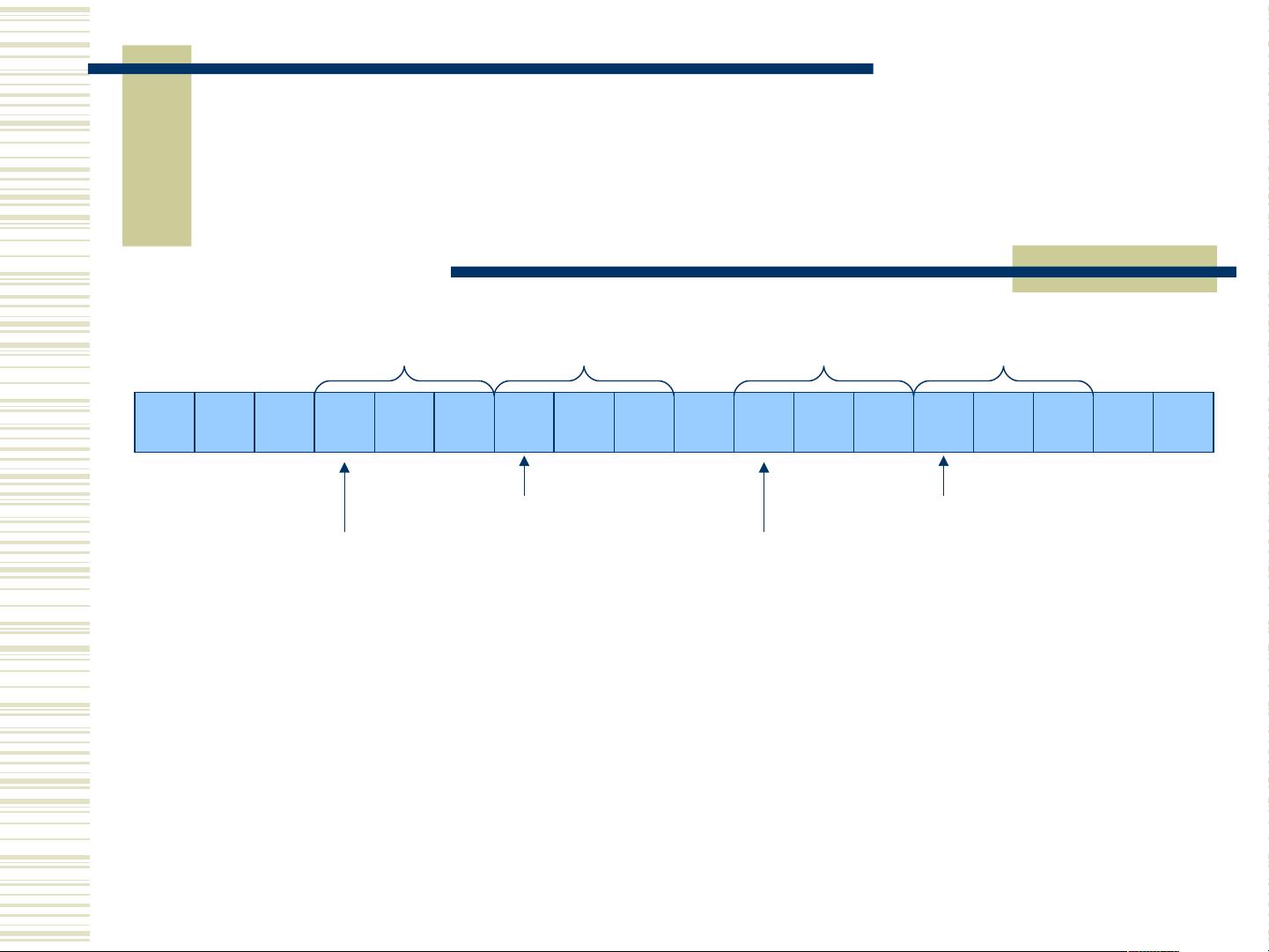 2. 采用倍增策略，定义uk为字符串u的前缀，根据定义的前缀比较关系<k, =k, 和≤k，对后缀进行逐级细化比较。 3. 在2k-前缀意义下比较后缀u和v，可以通过比较uk和vk，以及Suffix(i+k)和Suffix(j+k)来实现。 4. 重复上述过程，每次增大k的值，直到达到目标排序精度。 通过这种构造方法，后缀数组成为了处理字符串问题的强大工具，特别是在模式匹配、最长公共子序列、最长重复子串等问题上，后缀数组的应用显著提高了算法的性能，使其成为现代字符串处理研究中的核心内容。