B树与B-树详解:数据结构的平衡搜索算法
数据结构中的B树与B+树是两种重要的多路搜索树,它们在数据库管理系统(DBMS)和文件系统中广泛应用,以实现高效的查找、插入和删除操作。B树起源于二叉搜索树,但扩展了每个节点可以拥有的子节点数量,从而保证了数据的均衡分布和快速访问。
1. B树(Binary Tree):
- B树是二叉搜索树的一种变体,非叶子节点最多有两个子节点(左和右),遵循左指针指向小于关键字的子树,右指针指向大于关键字的子树规则。
- B树的优势在于通过保持节点的平衡,搜索性能接近于二分查找,而且插入和删除操作的开销相对较小,即使在树结构发生变化时,也不需要大规模移动数据。
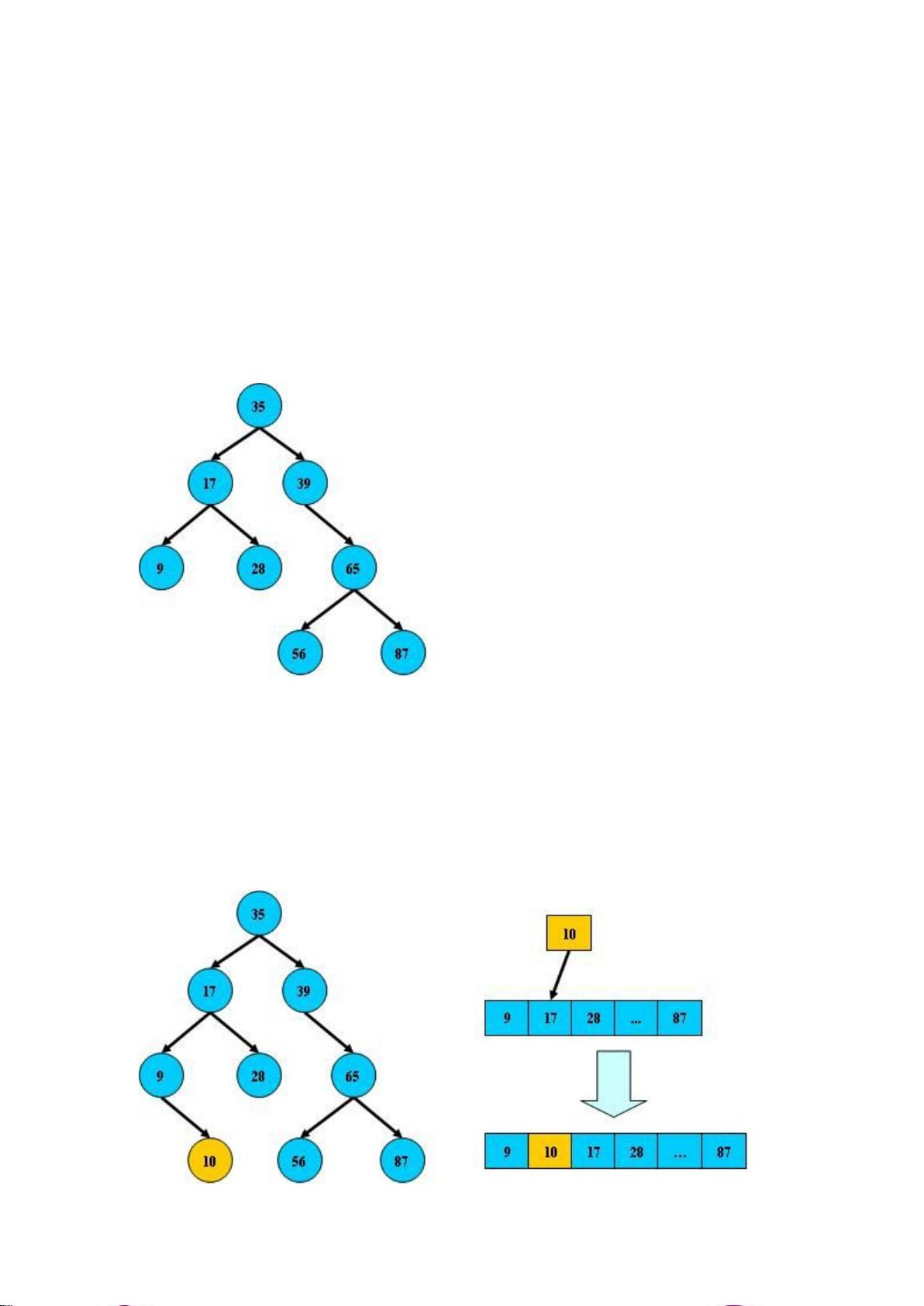
2. 不平衡的B树问题:
- 长期插入和删除可能导致B树的不平衡,例如像右图所示,这会导致搜索性能下降,表现为线性时间复杂度。
- 保持B树结构的“平衡”至关重要,实际应用中会采用平衡二叉树的策略,通过特定的平衡算法来维护节点间的均匀分布。
3. B-树(B-Tree):
- B-树是一种多路搜索树,非叶子节点的最大子节点数为M(M>2),具有更强的扩展性。
- 根节点的儿子数在[2,M]范围内,其他非叶子节点在[M/2,M]之间。
- 每个节点包含至少M/2-1(向上取整)到M-1个关键字,并根据关键字大小组织子节点指针。
- 所有叶子节点位于同一层,使得查找过程类似于对有序关键字序列进行二分查找。
- B-树的关键特性在于其更广泛的子节点分布,这使得它在处理大量数据时表现出色,同时保持了较高的查找效率。
4. B+树(B+ Tree):
- B+树是对B-树的进一步优化,所有数据都存储在叶子节点,而非叶子节点仅用于索引。这样,查找、插入和删除操作通常只涉及叶子节点,减少了磁盘I/O次数。
- 这使得B+树特别适合于文件系统,因为它在磁盘上的物理布局更有利于随机访问。
总结:
B树和B+树是数据结构中的核心元素,它们在解决海量数据存储和高效查找的问题上发挥着关键作用。通过控制节点的子节点数量、关键字的分布以及叶子节点的特性,B-树和B+树能够在各种场景下提供优秀的性能。理解和掌握这些数据结构对于数据库和文件系统的设计至关重要。同时,理解如何实现和维护平衡是确保其高效运行的关键。
点击了解资源详情
点击了解资源详情
点击了解资源详情
103 浏览量
2023-09-20 上传
2020-09-09 上传
2010-07-29 上传
2023-02-13 上传
咸鱼书生
- 粉丝: 0
- 资源: 17
最新资源
- R语言中workflows包的建模工作流程解析
- Vue统计工具项目配置与开发指南
- 基于Spearman相关性的协同过滤推荐引擎分析
- Git基础教程:掌握版本控制精髓
- RISCBoy: 探索开源便携游戏机的设计与实现
- iOS截图功能案例:TKImageView源码分析
- knowhow-shell: 基于脚本自动化作业的完整tty解释器
- 2011版Flash幻灯片管理系统:多格式图片支持
- Khuli-Hawa计划:城市空气质量与噪音水平记录
- D3-charts:轻松定制笛卡尔图表与动态更新功能
- 红酒品质数据集深度分析与应用
- BlueUtils: 经典蓝牙操作全流程封装库的介绍
- Typeout:简化文本到HTML的转换工具介绍与使用
- LeetCode动态规划面试题494解法精讲
- Android开发中RxJava与Retrofit的网络请求封装实践
- React-Webpack沙箱环境搭建与配置指南