有向图邻接矩阵与邻接表转换实战
需积分: 2 147 浏览量
更新于2024-08-05
1
收藏 55KB DOCX 举报
在数据结构的学习过程中,理解并掌握图的两种主要存储方式——邻接矩阵和邻接表是非常重要的。本篇内容主要围绕这两个概念展开,通过实践性的编程任务来深入剖析它们。
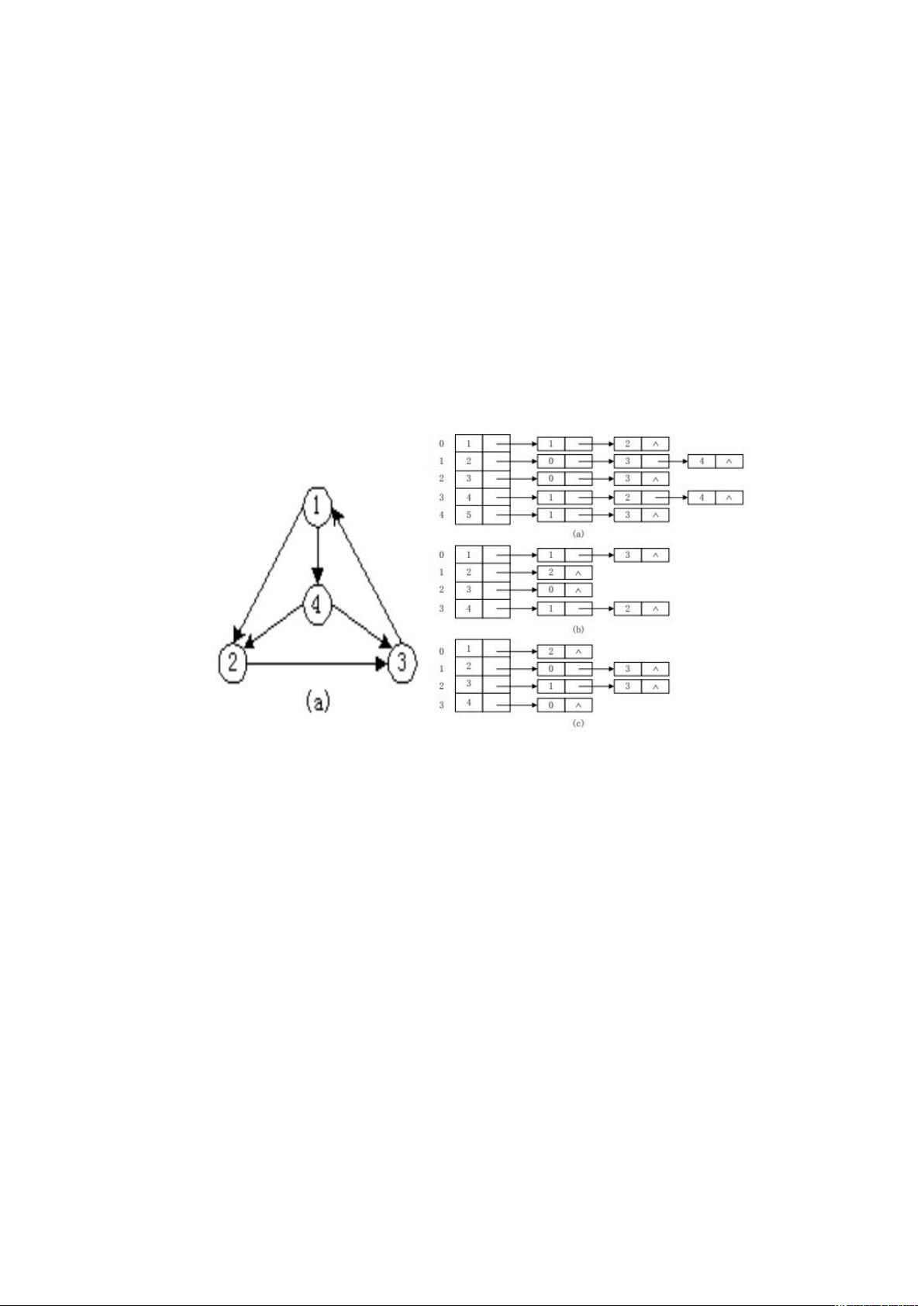
首先,邻接矩阵是一种二维数组结构,用于表示图中的顶点与顶点之间的关系。在这个矩阵中,行代表起点,列代表终点,矩阵元素的值表示对应边的存在与否(通常是1或0,或特定值表示不存在)。这种方法适合于稠密图,即边的数量接近于可能的最大边数,因为矩阵的空间效率较高,且查找任意两个顶点之间是否有边的操作时间复杂度为O(1)。
邻接表则是基于链表的存储结构,它使用一个数组或列表来存储每个顶点的所有邻接顶点,对于稀疏图(边的数量远少于可能的最大边数)更为高效。邻接表通常包含两个部分:顶点表(存储所有顶点及其数据)和边的链表,链表中的每个节点表示一条边,指向目标顶点,这样查找特定边的时间复杂度变为O(deg(v)),其中deg(v)是目标顶点的度数。
题目要求实现两个程序:第一个程序将给定的有向图存储为邻接矩阵,然后转换成邻接表并打印输出;第二个程序则相反,先以邻接表的形式存储,再转换为邻接矩阵。为了达到这一目标,设计的程序需要包括以下几个关键步骤:
1. 定义数据结构:
- 邻接矩阵使用`AdjMatrix`作为数组,`MGraph`结构体包含了顶点数组、邻接矩阵、顶点数和弧数。
- 邻接表使用`ArcNode`结构表示边节点,包含目标顶点和附加信息;`AdjList`数组存储顶点及其对应的边链表,`ALGraph`结构体包含邻接表、顶点数和弧数。
2. 输入操作:
- 手动输入图形信息,例如顶点和边的连接,可以采用用户交互的方式实现,根据选择的存储方式填充相应的数据结构。
3. 存储与转换:
- 对于邻接矩阵,遍历输入的顶点和边信息,更新矩阵元素。
- 转换邻接矩阵到邻接表时,需要遍历矩阵,为每个顶点创建新的边节点,并将其添加到相应顶点的链表中。
- 对于邻接表到邻接矩阵,遍历邻接表,根据链表中的目标顶点索引填充矩阵。
4. 输出:
- 打印转换后的数据结构,如邻接矩阵的元素或邻接表的边信息。
通过这个练习,学习者不仅能够掌握图的邻接矩阵和邻接表的基本概念,还能锻炼算法设计和数据结构实现的能力,以及在不同数据结构间的转换技巧。同时,理解何时选择邻接矩阵,何时选择邻接表,对于优化图的处理和分析至关重要。
2009-05-14 上传
2023-02-26 上传
2023-10-20 上传
2023-06-09 上传
2023-04-15 上传
2024-10-27 上传
2024-05-14 上传
白茶丫
- 粉丝: 5w+
- 资源: 1994
最新资源
- FindSport2Play:这是一个MERN Stack应用程序,玩家可以在其中举办活动,其他玩家可以参加并聚会以一起参加任何体育运动
- Microblaze-USB104A7_Video:USB104A7上的图像处理pipeleine
- fe-2006
- 合并多个Excel文件.zip易语言项目例子源码下载
- 多维度揭示心力衰竭患者生存关键因素(代码+数据)
- 模板工程.zip
- retro-board
- sharply:块状C#编辑器
- Java-Application-using-Spatial-Database:数据库系统
- Olimex-ESP32-POE-example:Olimex存储库中缺少的此示例程序提供了一个使用ESP-IDF 4.1及更高版本(初始化以太网子系统)的简单示例。 ESP-IDF 4.1有许多重大更改,因此一个有效的示例非常重要
- rfid的应用场景.zip
- regalstaket-mobler
- auth-boilerplate-with-redux
- sax:用于XML和HTML的sax-js sax样式解析器的维护分支
- FM-Intro-Component:使用CSS Grid,Flexbox和JavaScript表单验证的前端向导挑战
- 旅游及票务网站模版