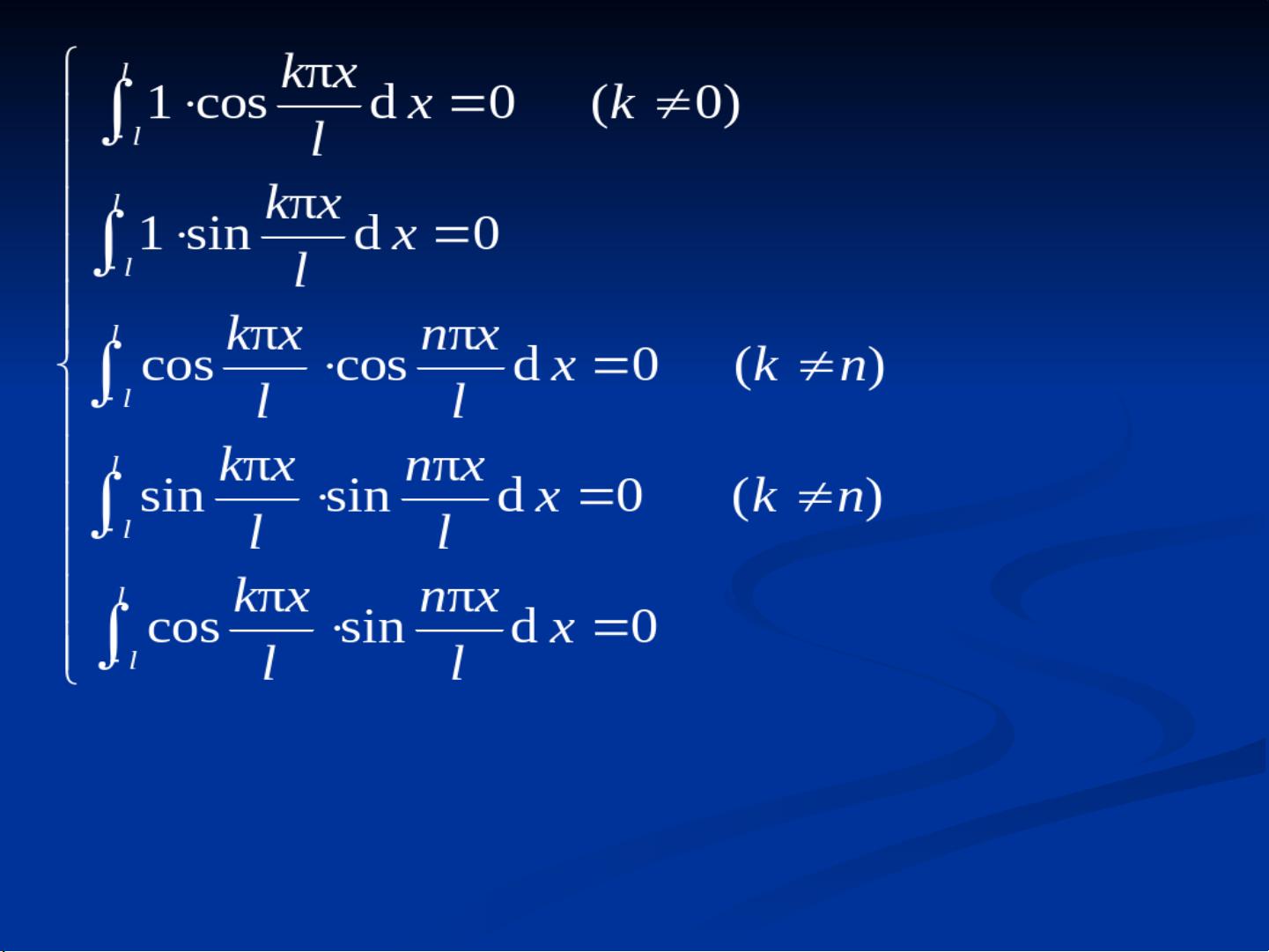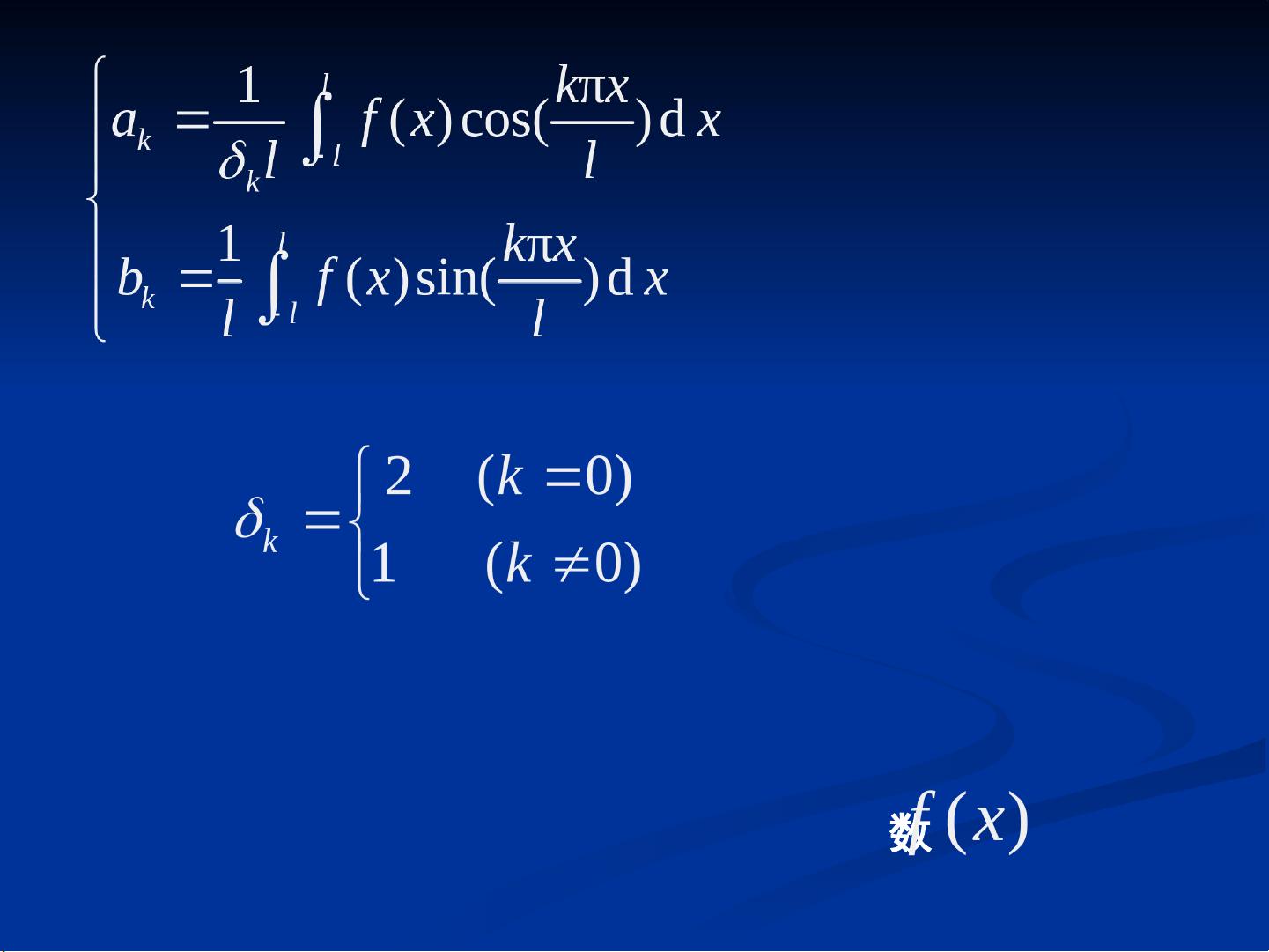积分变换揭秘：傅里叶变换与拉普拉斯变换的应用

"傅里叶变换是数学中的一种积分变换，它在多个科学和技术领域有着广泛应用，特别是在解决微分方程和信号处理方面。通过傅里叶变换，复杂的微分运算可以转换为简单的乘法运算，使问题的解决更为便捷。傅里叶变换的核心是通过特定的积分形式将一个函数转换为其像函数，而这个过程涉及到一个被称为核的函数。不同的核函数会产生不同的积分变换，例如傅里叶变换和拉普拉斯变换。傅里叶变换的核函数为指数函数，而拉普拉斯变换的核函数则是指数函数与时间的乘积。这两个变换在处理常微分方程和偏微分方程时有各自的优点，可以将问题转换为更易于求解的形式。傅里叶变换尤其在信号分析和光学中占据重要地位，而拉普拉斯变换则常见于控制系统和电路分析。" 傅里叶变换是一种强大的数学工具，它能够将一个在时间或空间域内的函数转换到频率域中，揭示出信号的频率成分。在描述中提到，傅里叶变换将复杂的微分运算转化为代数运算，这在解决微分方程，尤其是线性常微分方程和线性偏微分方程时非常有用。通过傅里叶变换，原本难以直接求解的问题可以转化为对像函数的处理，然后再通过逆变换得到原函数的解。 具体来说，傅里叶变换定义为： \[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt \] 其中 \( f(t) \) 是原函数，\( F(\omega) \) 是其傅里叶变换，\( \omega \) 表示频率，\( j \) 是虚数单位。这个变换将时间域内的函数转换到了频率域，使得我们能够分析信号的频率成分。 拉普拉斯变换则是另一种积分变换，它在控制理论和电路分析中常用，其定义为： \[ F(s) = \int_{0}^{\infty} f(t) e^{-st} dt \] 其中 \( s \) 是复数，包括实部 \( p \) 和虚部 \( j \omega \)，\( p \geq 0 \) 保证收敛。拉普拉斯变换在处理无穷区间上的函数时更具优势，可以将初值问题转化为更容易求解的形式。 傅里叶变换和拉普拉斯变换之间存在一定的联系，例如通过拉普拉斯变换可以推导出傅里叶变换，反之亦然。它们都是解决数学和物理问题的强大手段，能够简化复杂问题的求解过程，使得在信号处理、图像分析、通信工程等领域有广泛应用。