遗传算法求解二元函数最小值实例分析

本文档主要介绍了如何使用遗传算法来寻找二元函数的最小值。遗传算法是一种模拟自然选择和遗传过程的优化方法，常用于解决复杂的优化问题，如函数最小化。在这个例子中，目标函数是二元函数 y = x1^2 + x2^2，定义在区间 [-5, 5] 上。以下是关键步骤的详细解析： 1. **设置参数**： - NIND：初始种群的数量，即121个个体。 - NVAR：每个染色体（表示一个可能的解）包含的基因数量，这里是2个变量。 - PRECI：变量的二进制位数，表示每个实数值精度，这里是20位。 - MAXGEN：最大遗传代数，即算法会运行200代。 - GGAP：代沟，代表父代与子代遗传概率，设为0.8。 2. **初始化**： - 创建初始种群 Chrom，使用 crtbp 函数生成具有指定位数的随机二进制编码。 - 定义区域描述符 FieldD，包含了二进制位数、变量范围和边界条件。 3. **遗传操作**： - **适应度评估**：计算每个个体（染色体）的适应度值，这里使用 ranking 函数进行排序。 - **选择**：通过 'sus' 选择策略（如轮盘赌选择）挑选一部分个体作为父代。 - **重组**：使用 'xovsp' 重组方法（交叉）生成新的可能解。 - **变异**：应用变异操作（mut）以引入多样性，避免陷入局部最优。 4. **迭代过程**： - 每一代，将重组和变异后的子代与当前种群合并，通过 reins 函数进行替换。 - 记录每一代的最优解（最小值）和平均值，存储在 trace 数组中。 - 重复此过程直到达到最大遗传代数 MAXGEN。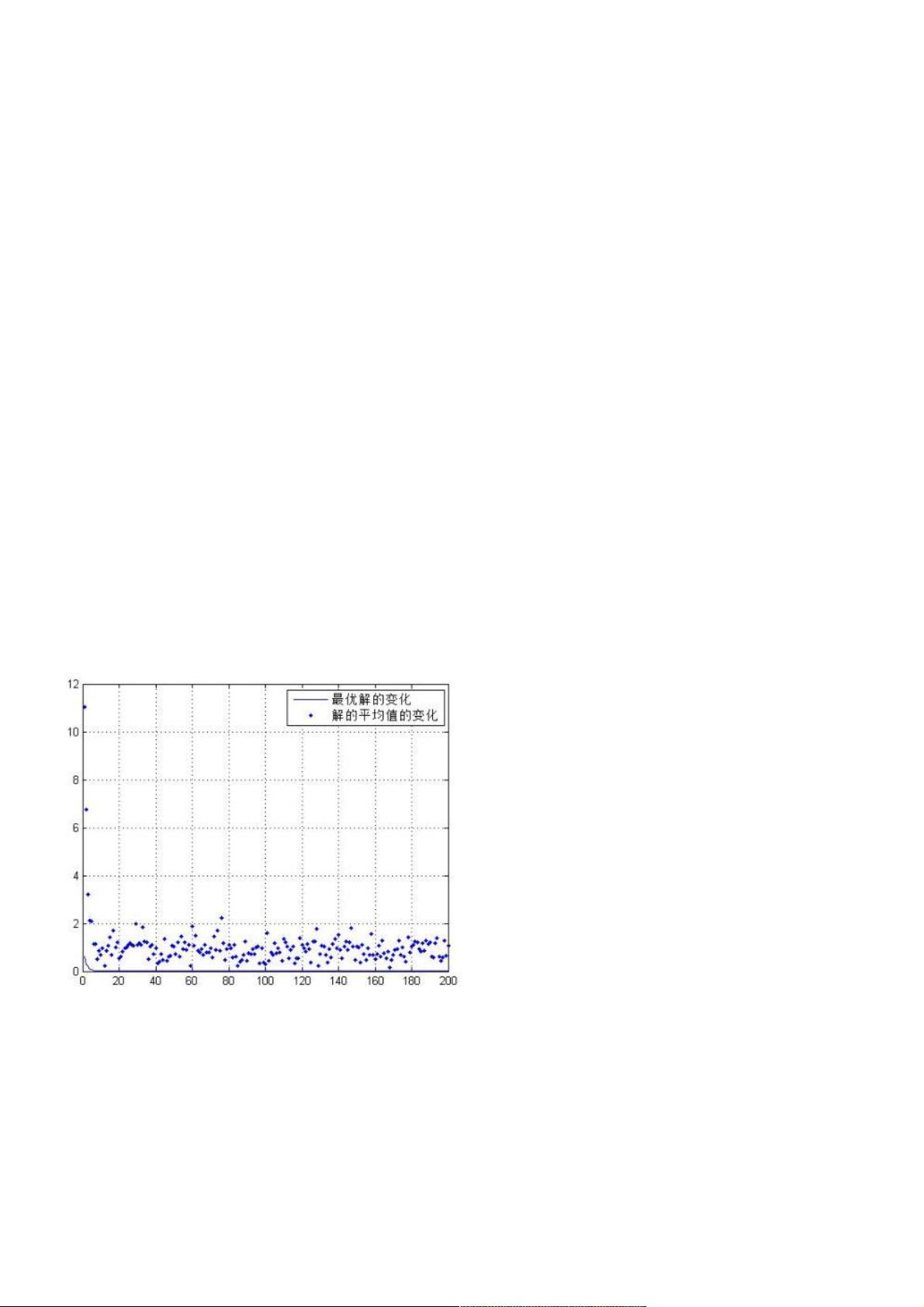 5. **可视化结果**： - 使用 plot 函数展示最优解的变化趋势和平均解的变化情况，以便观察算法收敛过程。 通过这个遗传算法模型，我们可以看到它如何通过不断迭代、优化和变异寻找二元函数的全局最小值。这是一种基于自然选择原理的非线性优化方法，对于解决复杂的优化问题具有一定的通用性和有效性。理解并运用这种算法，可以帮助我们优化各种实际问题中的决策变量组合，以找到最理想的解决方案。