哈夫曼树详解与构造过程

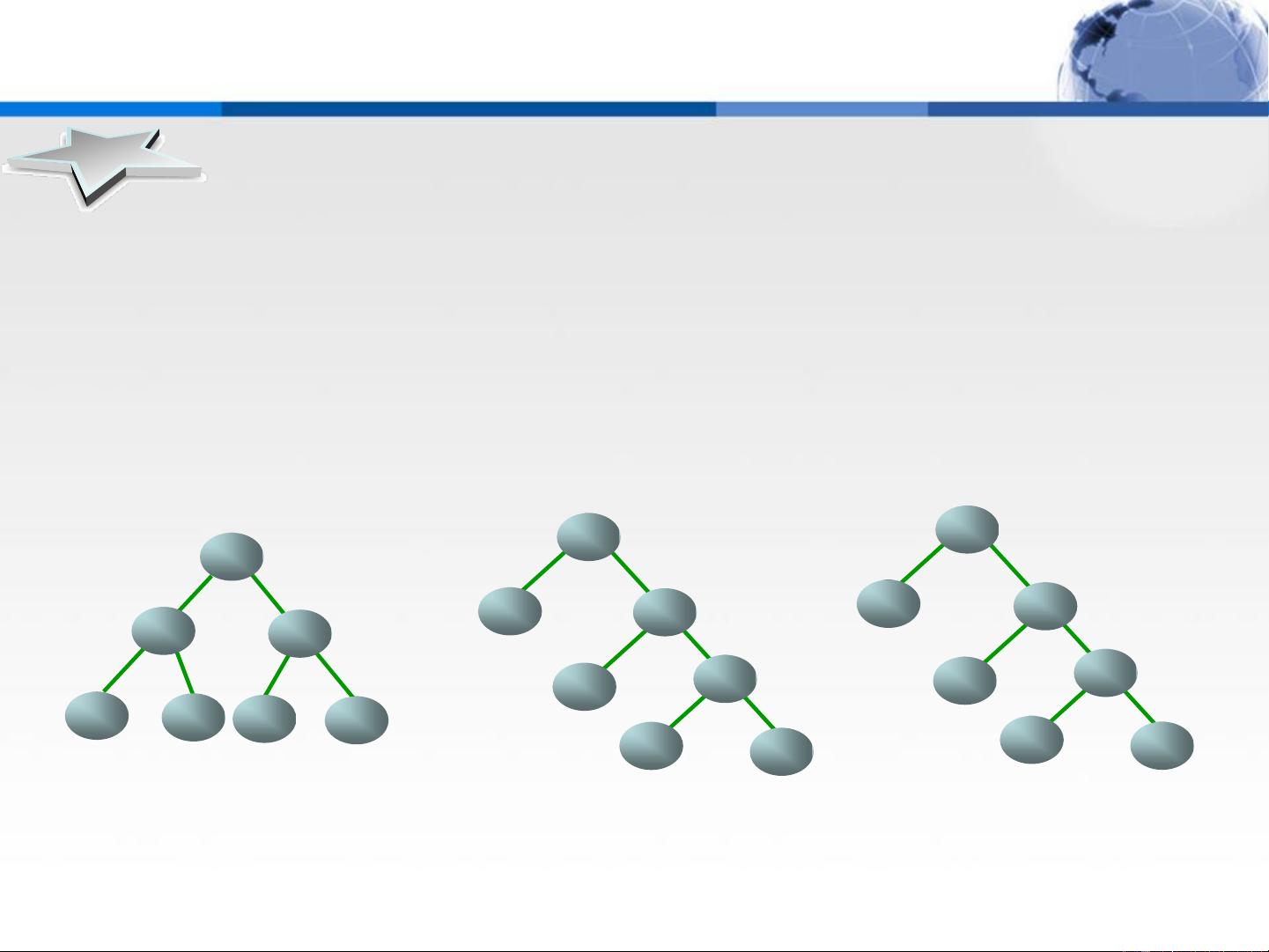
"本资源是关于数据结构中的哈夫曼树的讲解，主要涉及哈夫曼树的概念、应用以及哈夫曼编码的介绍。作者为gdou信息学院的BYMingGe，内容包括哈夫曼树的定义、带权路径长度、哈夫曼树的构建方法和哈夫曼算法的基本步骤。" 哈夫曼树是一种特殊的二叉树，它在数据压缩和编码中有着广泛的应用。在哈夫曼树中，叶子节点通常代表具有特定权值的数据元素，而权值则反映了这些元素的重要程度或频率。哈夫曼树的核心特性是它的带权路径长度（WPL）最小，即从根节点到所有叶子节点的路径长度与各自权值的乘积之和达到最小。 带权路径长度是计算哈夫曼树优劣的关键指标，公式表示为所有叶子节点的权值与其从根节点到叶子节点路径长度的乘积之和。例如，给定权值分别为2、3、4、7的四个叶子节点，可以构造出多种形状的二叉树，但哈夫曼树将是使得WPL最小的那棵。 哈夫曼树的构造通常通过哈夫曼算法实现，该算法包括以下四个步骤： 1. 初始化：根据给定的权值列表创建n棵只包含一个根节点的二叉树，构成集合F。 2. 选取与合并：从集合F中选取权值最小的两棵树，将它们合并为一棵新树，新树的权值为两棵子树的权值之和。 3. 删除与加入：删除被合并的两棵树，将新树加入集合F。 4. 重复以上步骤，直到集合F中只剩下一棵树，这棵树就是哈夫曼树。 在构造过程中，可以以示例的方式逐步展示这个过程，例如，对于权值集合{2, 4, 5, 3}，通过不断选择权值最小的两棵树进行合并，最终会得到一棵最优的哈夫曼树。 为了存储哈夫曼树，可以使用结构体来表示树的节点，结构体中包含节点的权值、左子节点、右子节点以及指向父节点的指针，以便于进行遍历和操作。这样的存储结构能够有效地支持哈夫曼树的构建和解码等操作。 总结来说，哈夫曼树是一种优化数据结构，通过构建最小带权路径长度的二叉树，实现高效的数据编码和压缩。了解并掌握哈夫曼树的原理和构建方法对于理解数据结构和算法，特别是在信息压缩领域的应用至关重要。