线性代数基础：解构、特性与向量表示

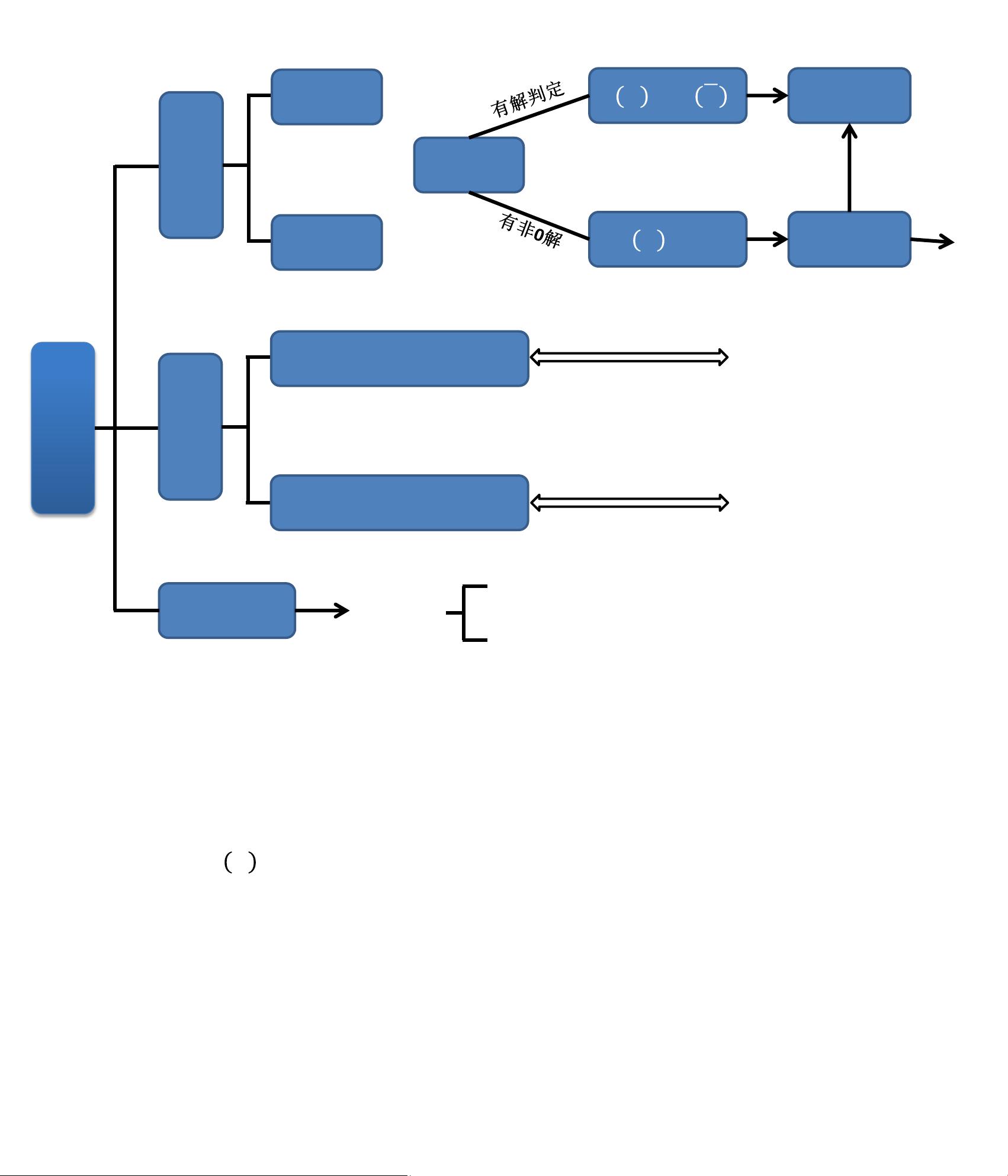
线性代数是数学的一个核心分支，它主要研究向量空间、线性变换、矩阵和它们之间的关系。本文档涵盖了线性代数的基本概念和核心理论，包括但不限于： 1. **方程组矩阵形式**：阐述了线性方程组 Ax = b 的基本表示，其中 A 是系数矩阵，x 是未知向量，b 是常数向量。这是解决线性系统的起点。 2. **阶梯形矩阵与秩（r(A))**：矩阵经过初等行变换后，变成阶梯形表示，即上三角或下三角形式。秩 r(A) 描述了矩阵的秩次，表示矩阵独立行或列的个数，对于判断方程组解的存在性和唯一性至关重要。 3. **解的结构与基础解系**：基础解系是Ax = 0 方程组的解集合中一组线性无关的解向量，它们是解集的结构基础。特征向量是满足特定条件的特殊解，它们与矩阵的特征值紧密相关。 4. **特解与通解**：特解是方程组的某一特定解，而通解则是包含所有可能解的线性组合。自由变量是表示解的非唯一性，即方程组的参数部分。 5. **初等变换**：这些是通过加法、数乘和行交换等方式改变矩阵的形式，它们在简化问题、求解线性方程组和理解矩阵性质中扮演重要角色。 6. **逆矩阵与伴随矩阵**：矩阵的逆矩阵 A^-1 存在的条件是 r(A)=n (n 为矩阵的阶)，伴随矩阵 A* 用于求逆和计算行列式的运算。 7. **特征值与特征向量**：特征值和特征向量是矩阵的重要属性，它们反映了矩阵在空间中的旋转或缩放行为。计算特征值有助于理解矩阵的稳定性以及其对向量空间的映射。 8. **行列式与行列式性质**：行列式用来衡量矩阵的重要性，其性质包括行交换、倍加和提取公因子等，它们在判断矩阵性质和解线性系统时发挥关键作用。 9. **矩阵运算与求逆方法**：如矩阵的加法、乘法、幂运算以及通过伴随矩阵或分块矩阵的方法求逆。 10. **线性表示与线性相关性**：向量是否可以被其他向量线性表示，以及如何判定线性相关性，例如克莱姆法则和伴随矩阵求逆在这些问题中的应用。 11. **内积与正交性**：内积定义了向量间的相似度，正交向量则具有特殊的垂直关系，这对于处理向量空间尤为重要。 本文档涵盖了线性代数的基础理论，从矩阵表示到向量空间理论，再到解决线性方程组的方法，为深入理解和应用这一领域提供了全面的指导。