FPGA上复数浮点协方差矩阵的优化实现与预处理策略

在信号处理领域，协方差矩阵的计算是一项核心任务，尤其在多级嵌套维纳滤波器、空间谱估计和相干源分析中起着关键作用。传统的计算方式中，由于运算涉及到复数浮点乘法，每次乘法后数据位宽会翻倍，加上后续的加减运算可能导致数据溢出问题。这在FPGA（现场可编程门阵列）这样的资源受限平台上，造成了巨大挑战。 FPGA设计者通常会遇到位宽扩展的线性增长问题，随着采样点数的增多，协方差矩阵运算的核心部分——乘累加单元需求急剧增加，可能导致FPGA资源的过度消耗。为解决这个问题，一种常见的策略是对中间结果进行截断，通过移位操作将每次累加后的数值除以2，以防止溢出。这种处理方式虽然牺牲了一定的精度，但能够有效节省资源。 对于MUSIC算法等复数运算密集的应用，研究者们致力于寻找简化处理的方法。例如，通过对称阵列（如均匀线阵和均匀圆阵，特别是偶数阵元的情况）进行数据预处理，可以利用阵列的对称性将其转化为实数运算，如通过构造共轭对称的方向矩阵或线性变换矩阵。然而，奇数阵元的均匀圆阵由于阵列流型矩阵的特性，不能直接应用这些方法，需要将其转换为虚拟线阵，并依赖于第一类Bessel函数，这对硬件实现提出了更高的要求。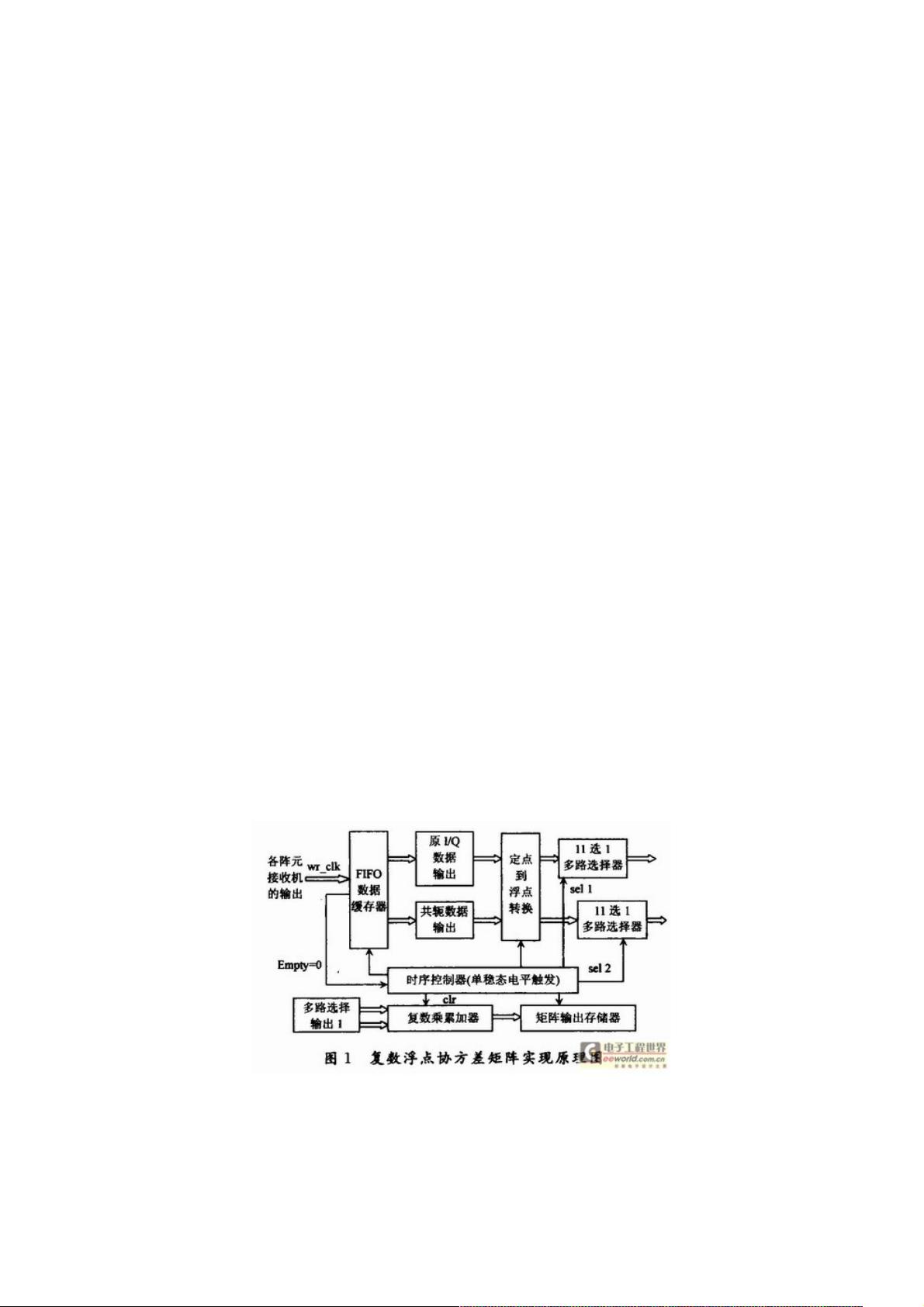 当处理奇数阵元的均匀圆阵时，尽管存在复杂性，但基于复数运算的协方差矩阵实现仍然是必要的。这促使研究人员寻求更加高效的复数浮点协方差矩阵在FPGA上的实现策略，可能包括优化算法设计、使用专用硬件加速器或者采用更先进的FPGA架构，如使用高带宽内存（BRAM）和Look-Up Tables (LUTs)来存储和处理复数数据。 总结来说，基于FPGA的复数浮点协方差矩阵实现是一个技术密集型的任务，需要权衡精度与资源利用，尤其是在处理不同阵列模型和阵元数目时，数据预处理和复数向实数转换的技术至关重要。通过巧妙的设计和优化，可以在保持算法性能的同时，有效降低FPGA资源的压力，为实际应用提供高性能的信号处理解决方案。