离散化设计：从连续到离散的转换方法

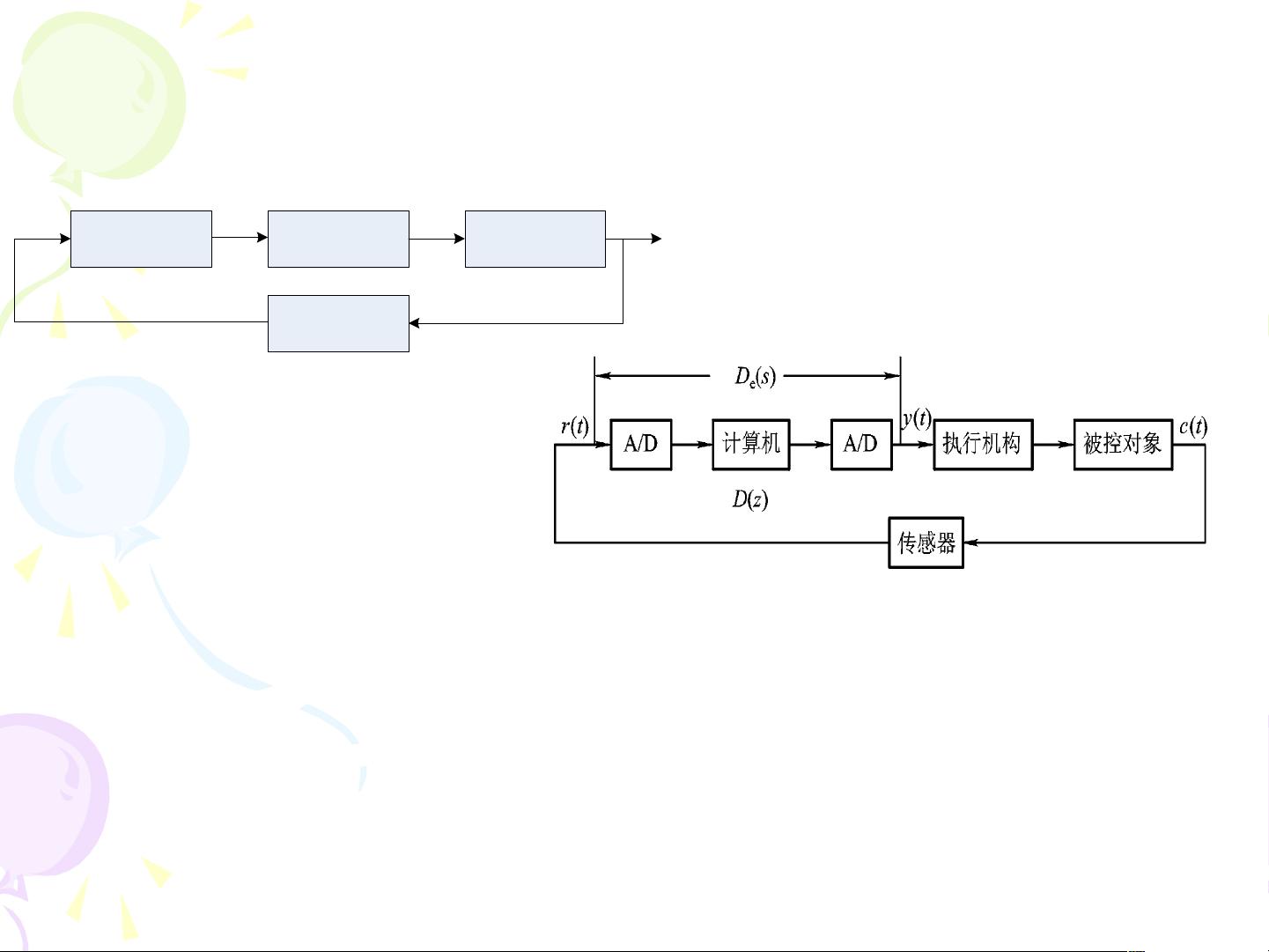
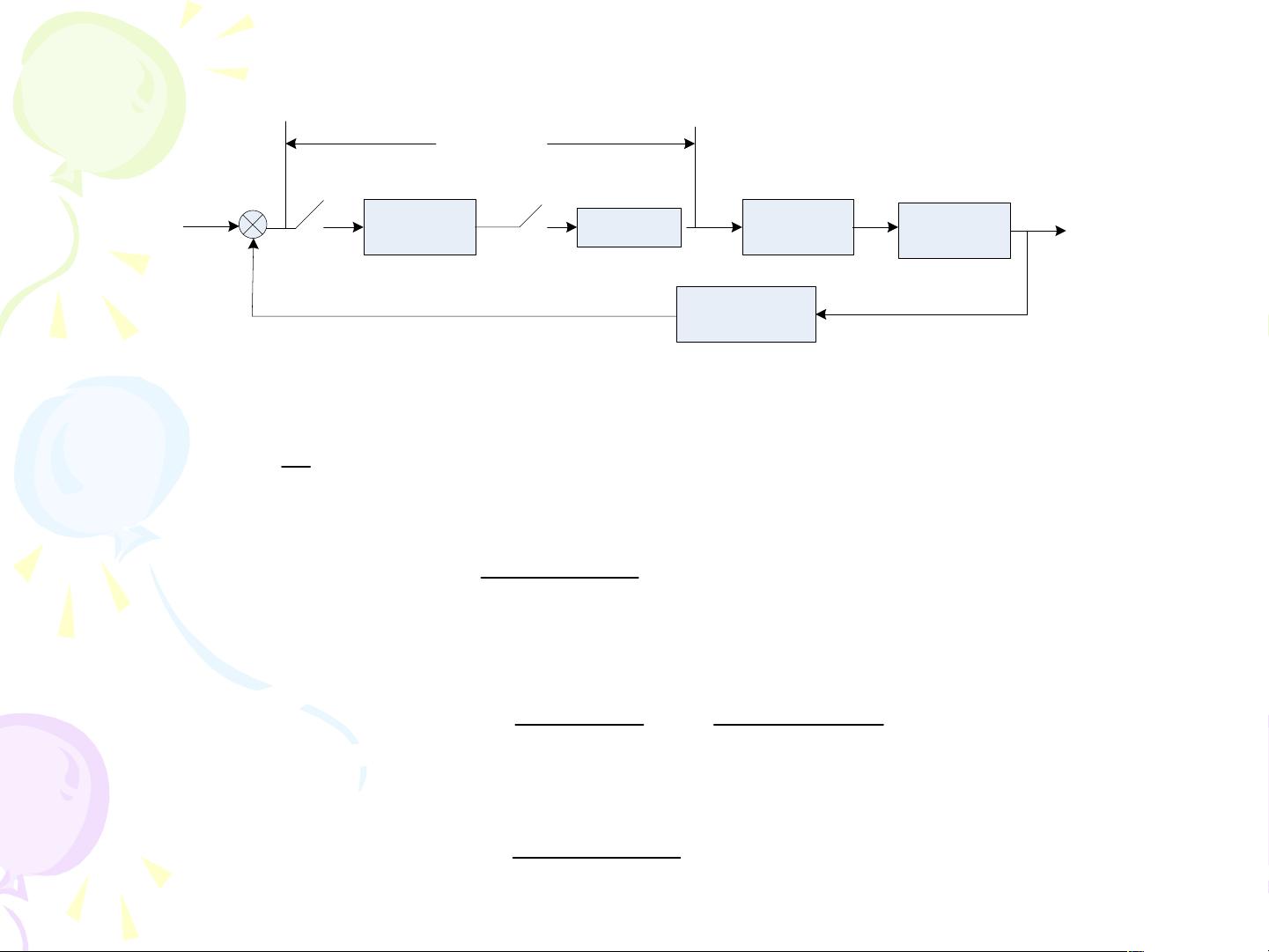
"离散化设计是将连续域中的控制理论应用于计算机控制系统的一种技术，尤其在飞行控制律的数字化设计中具有重要应用。通过离散化，可以将已知的连续控制律转换为适合计算机执行的离散形式。本文主要讨论了双线性变换等离散化方法，以及预修正双线性变换，并对几种变换方法进行了总结。" 离散化设计是计算机控制系统设计中的关键步骤，它允许我们把在连续时间域中设计的控制算法转换为离散时间域中的形式，以便在数字处理器上实现。这种方法在单输入单输出（SISO）系统的设计中尤为重要，如根轨迹设计和频率域设计。 双线性变换是一种常见的离散化方法，它提供了一种将连续传递函数转化为离散传递函数的手段。在双线性变换中，通常将连续控制律D(s)转换为离散等效控制律De(z)，使得离散系统的动态特性尽可能接近于原始连续系统。这种方法的优点在于，可以利用现有的连续系统分析和设计经验，且转换过程相对简单，结果明确。 预修正双线性变换是双线性变换的一个变种，它通过在变换前引入预修正式，以改善离散系统性能，尤其是减小超调和增加稳定性裕度。这种预修正通常涉及到对原始连续传递函数的预处理，以适应特定的离散化需求。 在离散域设计中，数字PID控制器设计是一个重要部分。与传统的模拟PID控制器相比，数字PID控制器通过采样周期控制信号，实现对系统响应的精确控制。此外，控制系统在z平面上的设计需要考虑性能指标，例如根轨迹设计和w'变换，这些方法有助于优化系统的稳定性和响应速度。 离散化设计的典型步骤包括：首先在连续域内设计控制律，然后采用适当的离散化方法（如双线性变换）将其转换为离散形式，最后评估和调整离散系统的性能，确保满足工程应用的需求。在实际应用中，ZOH（零阶保持器）常用于模拟到数字信号的转换，其传递函数可以表示为一个s和z之间的关系，这在计算离散等效控制律时起着关键作用。 离散化设计，特别是双线性变换及其预修正形式，是实现复杂控制策略，如飞行控制系统的数字化设计，以及多变量控制问题的关键技术。通过理解并熟练掌握这些方法，工程师能够有效地将连续控制理论应用于实际的数字控制系统。