气象数据分析：从相关系数到SVD分析

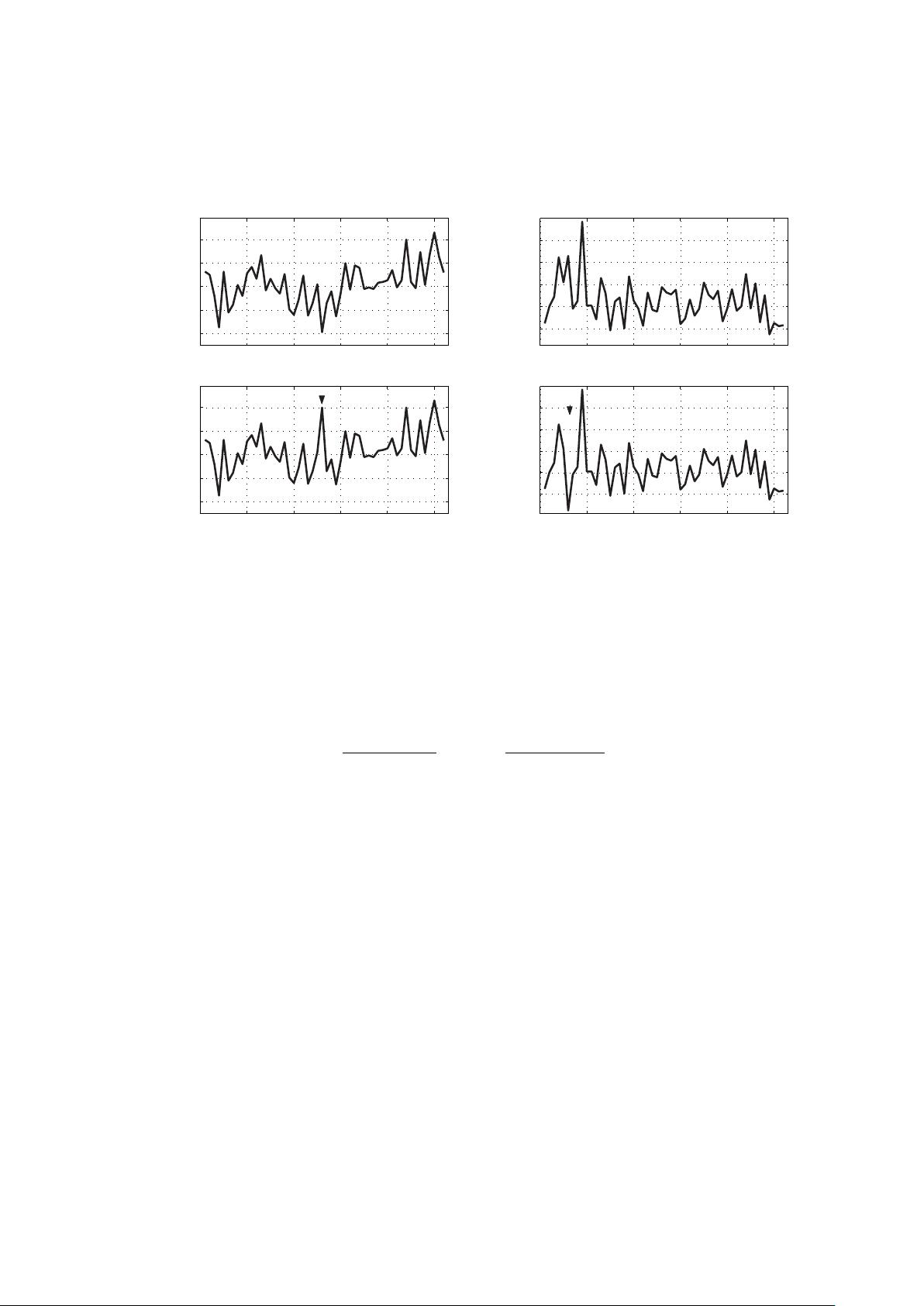
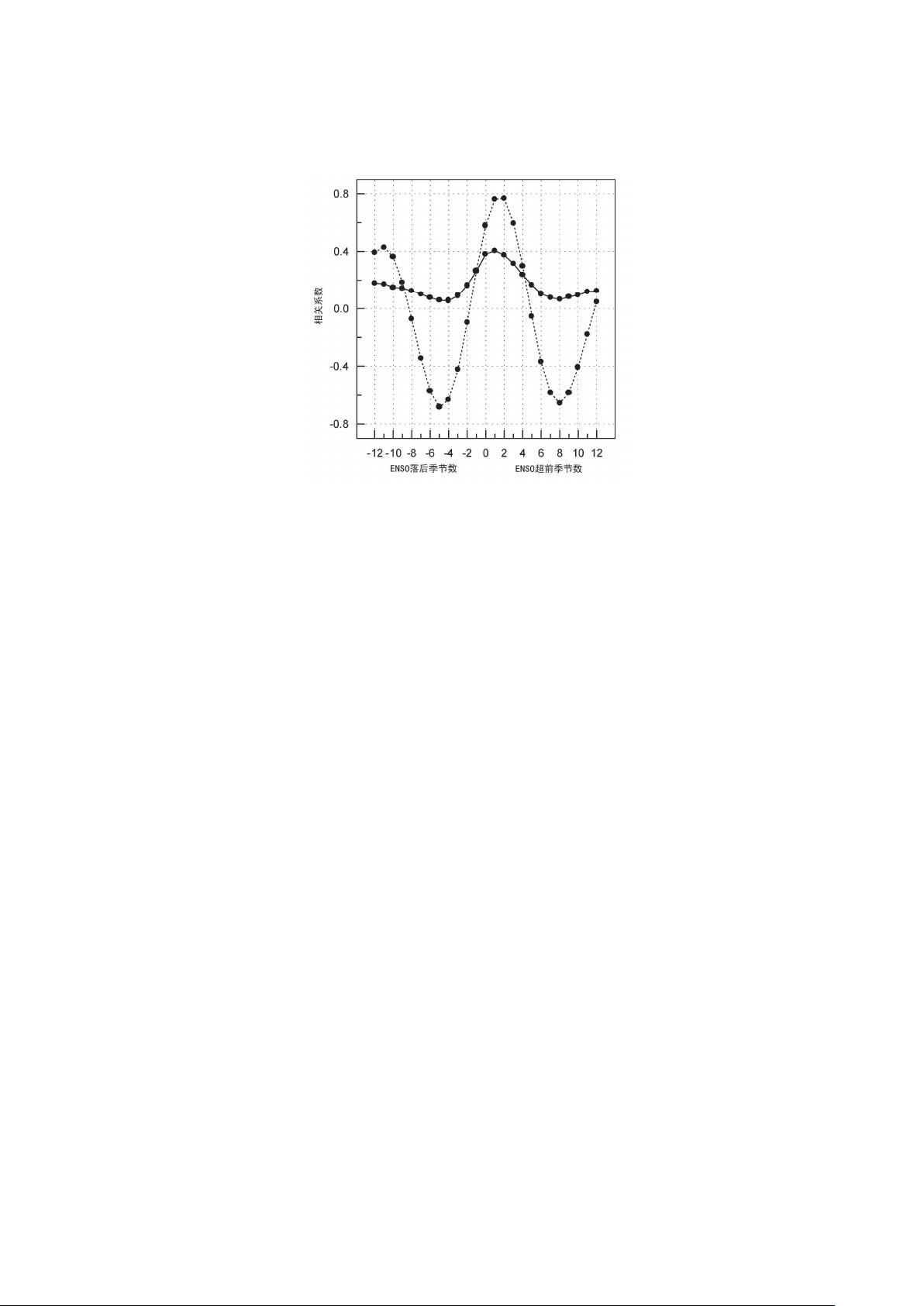
"该资源是一份关于气象数据分析的综合指南，特别关注小波处理技术的应用。文档涵盖了多种分析方法，包括但不限于普通相关系数、秩相关系数、谐波分析、功率谱分析、交叉谱分析、时间序列滤波分析、EOF（主成分分析）以及SVD（奇异值分解）等。此外，还提供了多个实例和图表来展示这些方法在实际气象数据中的应用，如北京夏季气温和降水的关系、ENSO指数与全球温度的滞后相关性、沙尘暴与850hPa高度高频变率方差的相关性等。文档中还包含了各种统计表，如Z统计表、相关系数检验表和有效自由度估计，以及详细的计算示例，帮助理解数据分析过程。" 在气象数据分析中，小波处理是一种强大的工具，它能够揭示数据在不同尺度和时间上的特征。小波分析可以用于捕捉信号的局部特性，尤其适用于非平稳和多尺度的数据，如气候变化或极端天气事件的研究。 1. 普通相关系数（Pearson相关系数）：它是衡量两个变量之间线性关系强度的标准度量，值介于-1到1之间。如果r接近1，表示正相关；接近-1，则表示负相关；r接近0表示没有明显线性关系。计算公式包括基于标准差的版本和基于积差的版本。 2. 秩相关系数：对于非正态分布或存在异常值的数据，秩相关系数（如Spearman's ρ或Kendall's τ）是一个更好的选择。它不依赖于变量的分布，而是基于变量的秩次，能捕捉变量间等级关系。 3. 谐波分析：在气象学中，谐波分析常用来研究周期性现象，如季节性变化。通过分解数据为不同频率的正弦和余弦波，可以了解数据的周期性和季节性模式。 4. 功率谱分析：功率谱展示了信号在频率域的能量分布，有助于识别隐藏的周期性或噪声特征，常用于气候变化研究和预测。 5. 交叉谱分析：这是一种分析两个时间序列共同频率成分的方法，可揭示它们之间的相位关系。 6. 时间序列滤波分析：通过滤波去除噪声，突出关键信号，如低通滤波用于提取长期趋势，高通滤波用于识别短期波动。 7. EOF（Empirical Orthogonal Functions，经验正交函数）分析，又称主成分分析，将多维数据转换为一组线性无关的主成分，便于识别数据的主要模式。 8. SVD（Singular Value Decomposition，奇异值分解）分析：用于降维和数据压缩，同时保持数据的主要信息，也可应用于气候数据的特征提取。 以上方法在气象数据分析中都有其独特的应用场景，结合实例和图表，这份合集为气象学家和相关研究人员提供了丰富的理论与实践指导。