使用 secant 法求解非线性方程

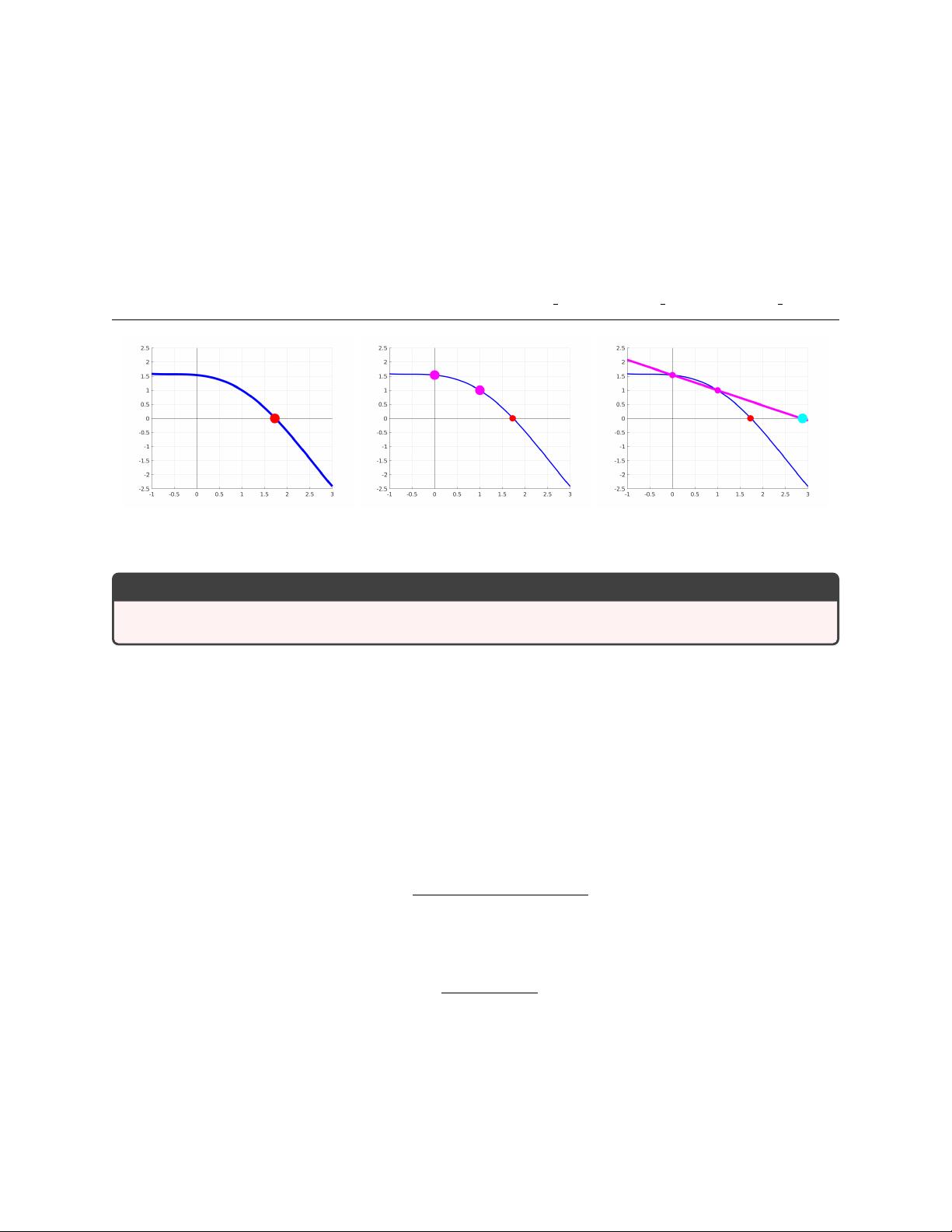
"非线性方程的割线法" 非线性方程是数学和科学计算中的一个核心问题，它们通常不能通过简单的代数运算直接求解。在数值方法领域，解决非线性方程的方法有很多种，其中割线法（Secant Method）是一种简单而实用的迭代方法。 割线法起源于16世纪，它是一种寻找函数零点（根）的数值方法，适用于连续且在目标零点附近可微的函数。该方法基于两点间的割线来逼近函数的根，其基本思想是利用两个已知点构造一条直线，然后通过这条直线预测下一个接近根的点。 具体步骤如下： 1. 首先需要选择两个初始点，通常我们称之为x₀和x₁，对应的函数值分别为f(x₀)和f(x₁)。这两个点不必满足变号条件，与二分法（Bisection Method）和牛顿法（Newton's Method）不同，割线法不强制要求初始区间内函数值变号。 2. 基于这两个点构建割线方程： y(x) = f(x₀) * (x - x₁) + f(x₁) * (x - x₀) 这是一条过点(x₀, f(x₀))和(x₁, f(x₁))的直线，理论上如果f(x)在这两点之间局部线性，那么这条割线能很好地近似函数。 3. 通过割线方程找到下一个迭代点x₂，它是割线与x轴交点的估计值，即： x₂ = x₁ - f(x₁) * (x₁ - x₀) / (f(x₁) - f(x₀)) 4. 检查x₂是否足够接近函数的根，如果不是，则用x₂替换之前的某一个点（通常是更远离根的那个点），然后重复步骤2和3，直到达到预定的精度要求。 割线法的优点在于它不需要初始区间有变号，而且代码实现相对简单。当初始点选取得足够靠近根时，它的收敛速度通常比二分法快。然而，如果初始点选择不当，割线法可能无法收敛或者收敛速度会变慢。此外，由于割线法是线性逼近，它可能在函数具有复杂结构或非单调性时表现不佳。 在实际应用中，为了提高稳定性和收敛速度，有时会采用改进的割线法，如：Hager's Rule、Fritsch-Carlson Rule等，这些规则可以帮助处理可能出现的异常情况，如倒退和振荡。 总结来说，割线法是一种用于求解非线性方程的有效数值方法，它依赖于两点间函数的线性插值来逐步逼近零点。虽然不如牛顿法或拟牛顿法那样具有全局收敛性，但割线法在很多情况下都能提供快速且可靠的解，特别是在没有函数导数信息或初始点选择合理的情况下。