"机器人学中的位置与姿态表示及变换"

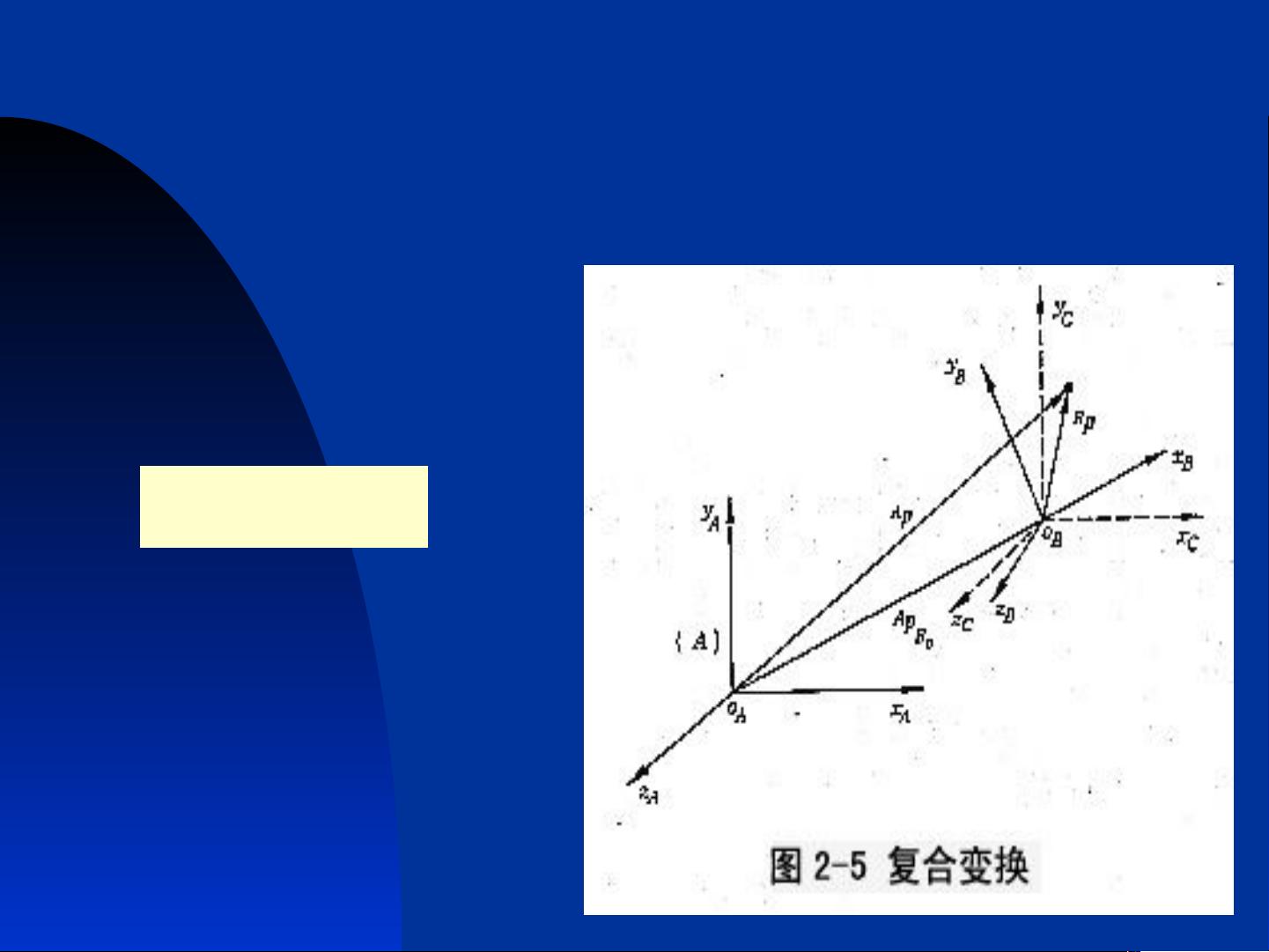
机器人学是研究机器人系统的一门学科，它涉及到许多基础的数学概念和原理。其中，位置与姿态的表达是机器人学中非常重要的内容之一。在机器人学中，位置描述和方位描述是描述机器人位置与姿态的常用方式。 位置描述使用直角坐标系来表示空间中任意一点的位置。它可以用一个3x1的列向量，也称为位置矢量，来表示。这个位置矢量包含了点在空间中的三个坐标值，分别是x、y和z。通过位置矢量，我们可以准确地确定机器人在空间中的位置。 方位描述则是用来描述机器人的方向或姿态。它是通过一个3x3的矩阵来表示的，这个矩阵称为旋转矩阵。旋转矩阵描述了一个由坐标系B相对于参考坐标系A的旋转变换。在旋转矩阵中，每一列代表坐标系B中某个单位主矢量相对于参考坐标系A的方向余弦。通过这个旋转矩阵，我们可以准确地确定机器人的方向。 在机器人学中，还有一些基础的数学知识和方法与位置和姿态的表示密切相关。其中，坐标变换是将一个坐标系中的点转换到另一个坐标系中的方法。它通过一个变换矩阵实现，这个变换矩阵包含了位置和方位的信息。齐次坐标变换则是一种常用的坐标变换方法，它将位置和方位统一表示为一个4x4的齐次坐标变换矩阵。物体的变换及逆变换是在坐标系中对物体位置和方位进行变换或逆变换的方法。通用旋转变换是一种将旋转变换表示为绕x、y和z轴的连续旋转变换的方法。 在机器人技术的数学基础中，对于位置和姿态的表示进行了详细介绍和讨论。通过对位置和姿态的表示方法的学习，我们可以准确地描述和把握机器人在空间中的位置和方向。这对于机器人的运动控制、路径规划和定位等技术具有重要意义。 总之，机器人学中的位置与姿态的表达是机器人技术中的基础知识之一。通过位置矢量和旋转矩阵，我们可以准确地描述和把握机器人在空间中的位置和方向。同时，通过坐标变换、齐次坐标变换和通用旋转变换等方法，我们可以对机器人的位置和姿态进行灵活的变换和控制。这些数学基础知识为机器人技术的发展和应用提供了重要的支持和保障。