递归与循环算法比较：效率与应用场景分析

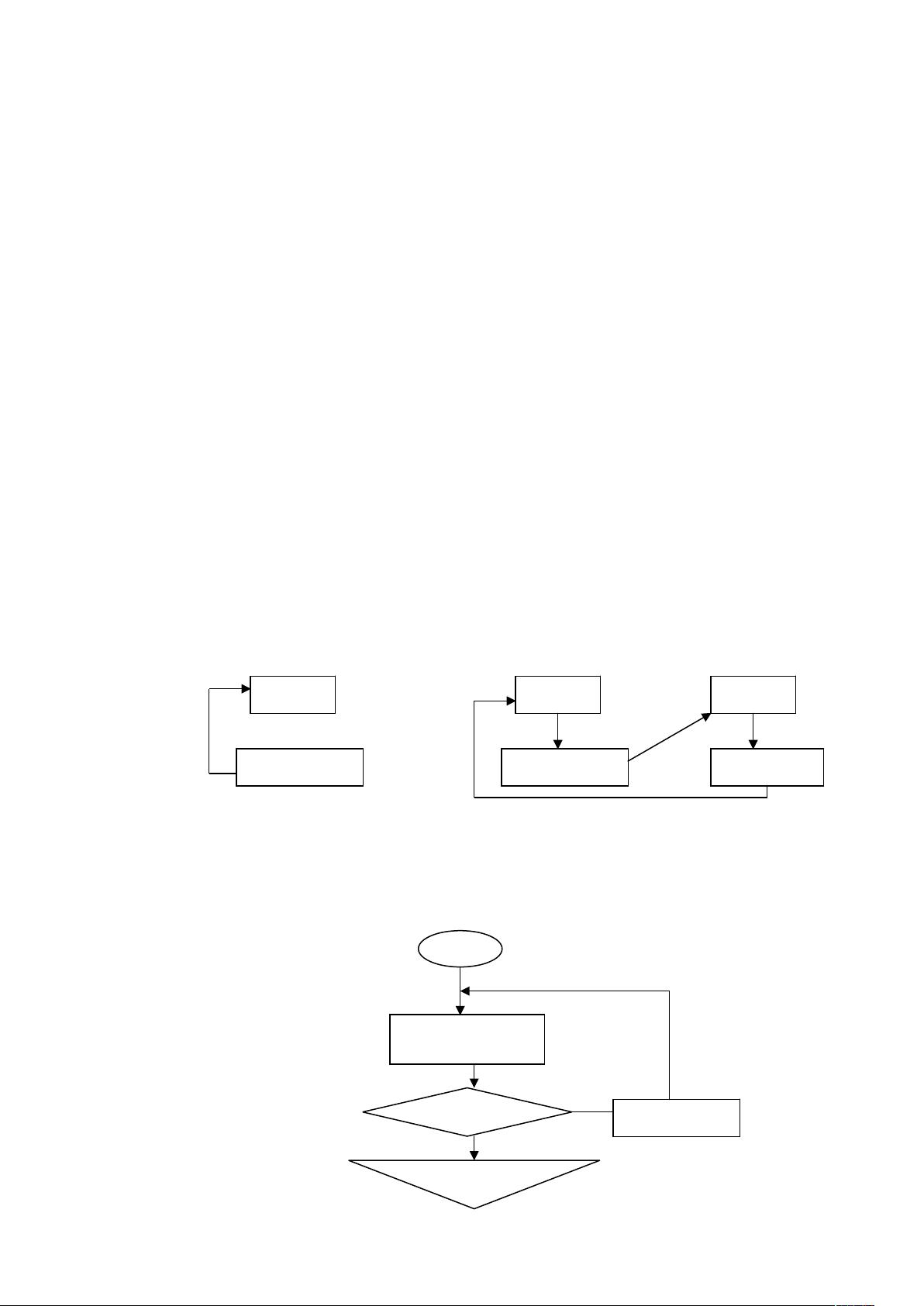
"递归算法与循环算法的分析" 在编程领域，递归算法与循环算法是两种常见的控制流程，它们各自具有独特的特性和适用场景。本文通过对递归和循环的详细解析，以及通过实例对比，旨在帮助开发者更好地理解这两种算法，并在实际编程中做出合适的选择。 1、递归算法 递归算法是一种自引用的编程方法，它在解决问题时会调用自身来解决子问题。递归通常涉及三个主要部分：基本情况（base case）、递归情况（recursive case）和递归调用。递归的优点在于代码简洁，易于理解，尤其适合处理分治策略的问题。然而，递归的缺点也很明显，比如可能导致大量的函数调用，增加时间复杂度，并占用更多的内存空间（栈空间）。在斐波那契数列的递归实现中，由于每次调用都会产生两个新的递归调用，导致时间复杂度为O(2^n)，效率较低。 2、循环算法 循环算法则是通过重复执行一段代码直到满足某个终止条件为止。循环结构包括while、for等，它们允许我们控制代码的执行次数，通常比递归更高效。例如，在斐波那契数列的循环实现中，我们只需要遍历一次序列，时间复杂度为O(n)，相比递归版本，效率显著提高。尽管循环可能使代码稍显复杂，但其性能优势在处理大数据量时尤为明显。 3、实例对比 在斐波那契数列的例子中，递归算法虽然直观，但由于重复计算，时间复杂度呈指数增长，不适用于大规模的n值。而循环算法通过迭代避免了重复计算，线性的时间复杂度使其在性能上远胜递归。 4、选择策略 在实际编程中，应根据问题的特性、效率要求和代码可读性来选择合适的算法。如果问题规模较小，且易于用递归表达，可以优先考虑递归；如果对效率有较高要求，或者问题可以通过迭代方式更有效地解决，则更适合使用循环。此外，还可以结合动态规划、记忆化搜索等技术优化递归算法，降低时间复杂度。 5、空间复杂度 除了时间复杂度，空间复杂度也是衡量算法性能的重要指标。递归算法由于需要维护函数调用栈，空间复杂度通常较高；而循环算法的空间复杂度通常与问题规模有关，往往较低。 总结来说，递归和循环各有优势，理解它们的工作原理和适用场景对于编写高效、易读的代码至关重要。在实践中，开发人员需要根据具体情况权衡两者，选择最适合的解决方案。