Dijkstra算法详解：最短路径探索与步骤演示

"最短路径算法——Dijkstra算法是一种用于寻找有向或无向加权图中两点间最短路径的经典算法。该算法的主要应用场景是网络路由选择，其中需要确定从源节点到其他所有节点的最短距离或时间成本。Dijkstra算法基于贪心策略，通过迭代的方式逐步优化路径长度。 算法流程分为两个关键步骤： 1. 初始化阶段：首先定义一个集合N，包含初始源节点（例如，图中的结点1）。对于不在集合N中的节点，赋予一个极大值（通常为正无穷），表示它们当前没有连接到源节点。在这个例子中，D(v)被初始化为99，表示到这些节点的距离未知。 2. 扩展阶段：每次从N的外部选择一个未访问过的节点w，它的D值（到源节点的距离）是最小的。将w加入到N中，然后更新与w相邻的所有节点v的D值，使其距离变为D(w)加上从w到v的边的权重（l(w, v)）。更新公式为：D(v) = min(D(v), D(w) + l(w, v))。这个过程会一直持续，直到N包含了所有节点为止。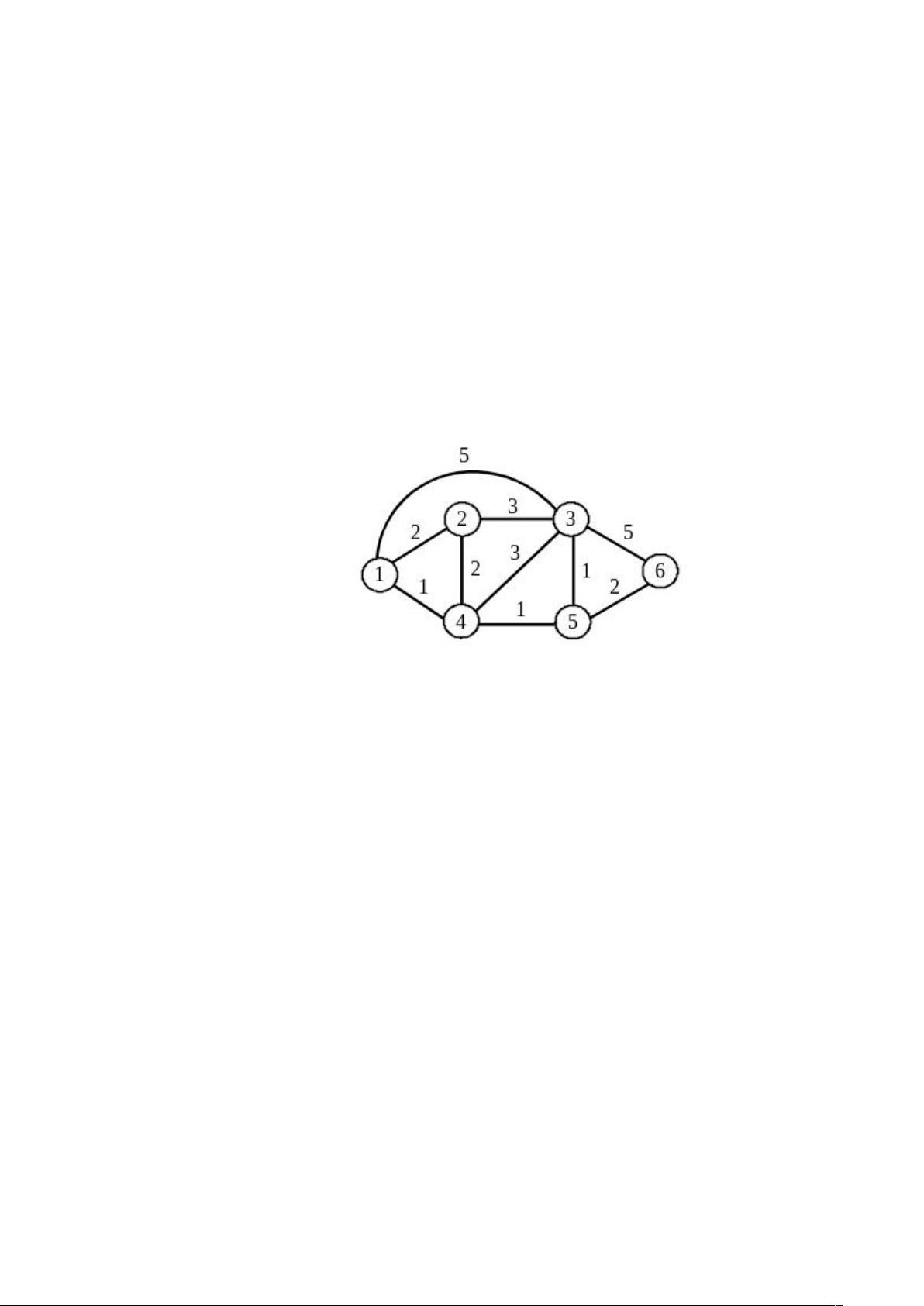 在给出的例子中，针对图E-1，算法从源节点1开始，依次找到各个节点的最短路径。每一步都会更新节点的距离值，直到所有节点都被纳入集合N。例如，在第四步，D(3)的最小值从1变为3，因为通过节点4可以到达节点3，且总距离更短。最后，当所有节点都在集合N中时，算法结束，此时已经找到了从源节点到所有其他节点的最短路径。 表E-1展示了求解过程中的详细步骤，每个节点的D值随算法的进行而逐渐更新，直到所有节点距离值稳定，显示了最短路径。在整个过程中，Dijkstra算法保证了找到的是网络中从源节点到其他节点的最短路径，其核心在于利用了贪心策略和优先级队列数据结构，使得搜索过程高效且正确。"