"第6章 整数规划1: 引入逻辑变量的需要及纯整数线性规划"

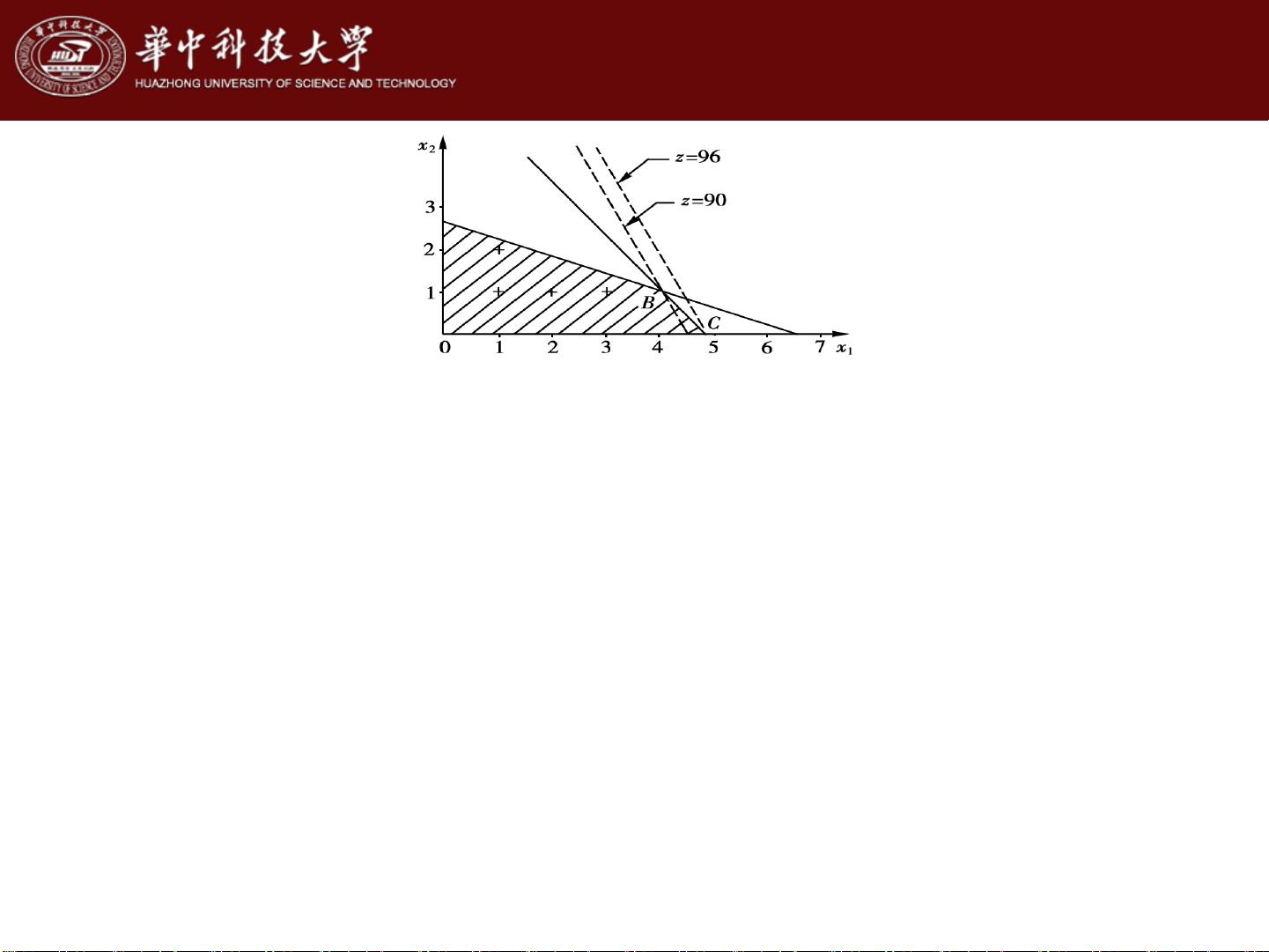
第6章 整数规划 第1节 整数线性规划问题的提出 在线性规划问题中，有时候对解答的要求是整数形式的。这样的问题被称为整数线性规划问题。整数线性规划问题是最近几十年来规划论中的一个重要分支。 整数线性规划问题的特征在于需要求解的变量必须是整数。这样的限制来自于问题本身的要求。例如，当我们需要求解机器的台数、完成工作的人数或装货的车数等时，只接受整数解是合理的。 整数线性规划问题的可行域是一个离散集合，即只有某些整数是允许的解，而分数或小数的解是不被接受的。 第2节 分支定界法 分支定界法是一种求解整数线性规划问题的常用方法。它基于以下思想：将整数线性规划问题转化为一系列线性规划问题，并通过对每个子问题的求解来逐步缩小解空间。 分支定界法首先将整数线性规划问题转化为一个线性规划问题，求解得到一个最优解。然后根据最优解的取值，将问题分解成两个子问题。分别以最优解取整后的下界和上界进行求解。 逐步分解之后，我们可以得到一个整数线性规划问题的可行解集合。通过递归的方式，不断缩小解空间，直至找到最优解。这种方法的时间复杂度较高，但可以保证找到最优解。 第3节 割平面法 割平面法是另一种求解整数线性规划问题的方法。它基于以下思想：通过添加一系列约束条件将问题的解空间划分为更小的可行域，从而得到更精确的解。 割平面法首先将整数线性规划问题转化为一个线性规划问题，求解得到一个最优解。然后通过添加与最优解不一致的约束条件，得到一个新的线性规划问题。再次求解这个新的线性规划问题，得到一个更精确的解。 通过不断添加约束条件和求解新的线性规划问题，最终可以得到一个整数线性规划问题的可行解集合。这种方法的时间复杂度相对较低，但并不能保证找到最优解。 第4节 0-1型整数线性规划 0-1型整数线性规划是一种特殊的整数线性规划问题，其中所有的变量都限制为0或1。0-1型整数线性规划在实际问题中有着广泛的应用。 0-1型整数线性规划问题可以转化为一个图论问题，通过图的遍历算法求解。其中，图的节点表示变量，边表示变量之间的关系。通过遍历图找到满足约束条件的解，即为问题的最优解。 第5节 指派问题 指派问题是一种特殊的0-1型整数线性规划问题。它是将n个任务分配给n个执行者的最优化问题。 指派问题可以通过枚举法求解，但这种方法的时间复杂度非常高。因此，通常采用匈牙利算法或网络流算法来解决指派问题。 第6章 整数规划总结 整数规划是在线性规划问题中的一个重要分支。它要求求解的变量必须是整数，而非分数或小数。整数规划的可行域是一个离散集合，求解整数规划问题需要采用特定的算法。 在整数规划问题中，常用的求解方法包括分支定界法和割平面法。分支定界法将整数规划问题转化为一系列线性规划问题，并通过对每个子问题的求解来逐步缩小解空间。割平面法则通过添加一系列约束条件将问题的解空间划分为更小的可行域。 对于特殊的整数规划问题，如0-1型整数线性规划和指派问题，还有针对性的解法。0-1型整数线性规划问题可以转化为图论问题，通过图的遍历算法求解。指派问题则可以通过匈牙利算法或网络流算法来解决。 总的来说，整数规划在实际问题中有着广泛的应用。通过合理选择求解方法，可以高效地解决整数规划问题，得到最优解。