自回归时间序列误差分位数估计与预测区间构建

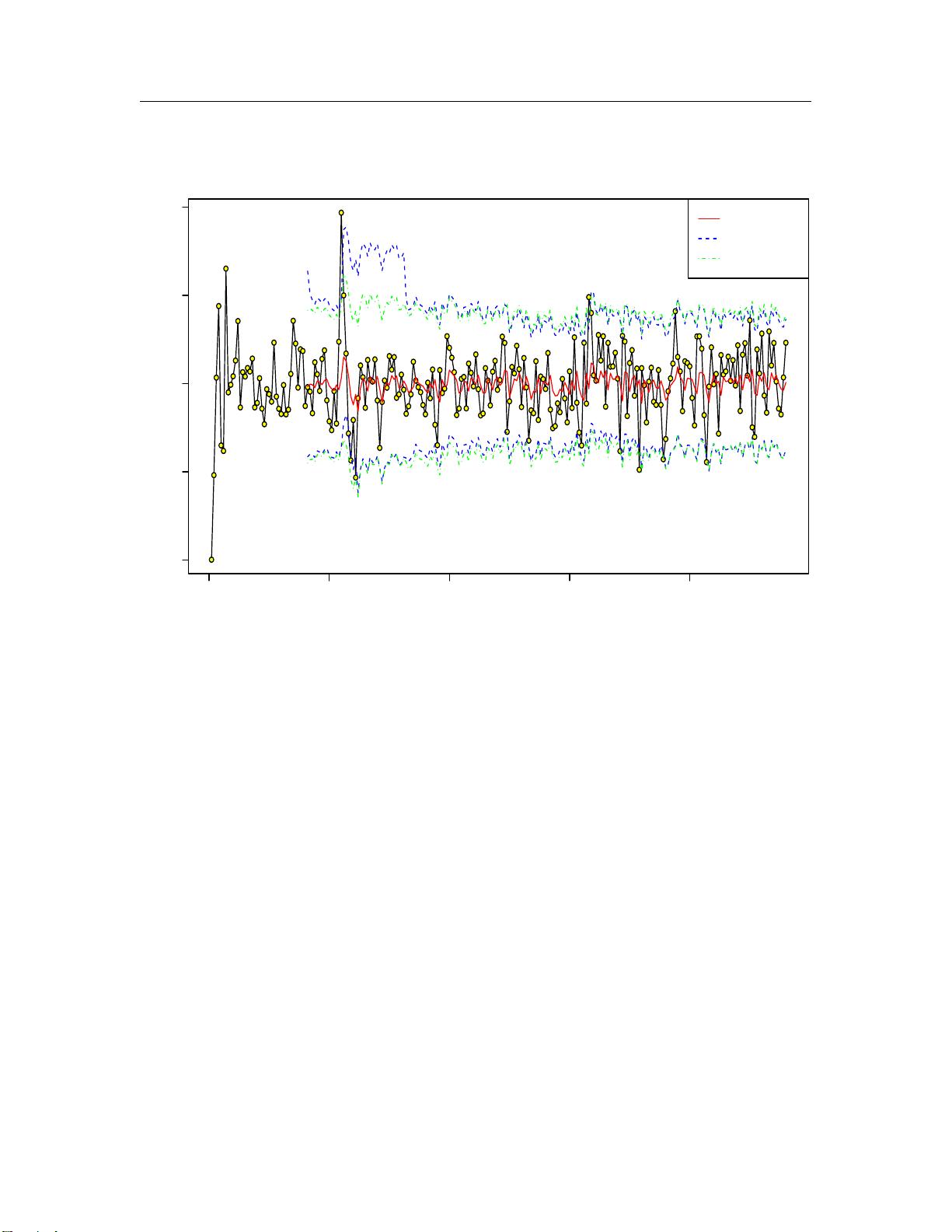
"这篇文章主要探讨了自回归时间序列AR(p)模型中误差分位数的高效估计和预测区间的构建。作者徐惠、杨立坚和沃尔夫冈哈德勒提出了一种新颖的方法，该方法结合了误差分布的核平滑估计与Yule-Walker方法来估计AR(p)模型的误差分位数。通过特定条件下的分析，他们证明了这个估计量在理论上是有效的，并且其渐近分布与真实误差分位数相同。此外，他们利用这个估计量构建了AR(p)模型的预测区间，并且能够确保在统计上达到预定的置信水平。通过大量模拟实验和实际数据的应用，文章的理论结果得到了验证。关键词包括AR(p)模型、窗宽选择、核函数以及残差处理。" 这篇论文的核心知识点包括： 1. **自回归时间序列AR(p)**: AR(p)模型是一种常用的时间序列分析模型，其中当前值依赖于过去的p个值。在AR(p)模型中，误差或创新项的性质对模型的性能和预测至关重要。 2. **误差分位数估计**：文章提出了一种新的估计方法，用于确定误差分布的分位数。这在理解时间序列的不确定性和异常值方面非常重要，因为不同的分位数可以提供关于数据分布形状和尾部厚度的信息。 3. **核平滑与Yule-Walker方法**：论文结合了这两种技术来估计误差分位数。核平滑是一种非参数统计方法，通过滑动窗口来估计数据的局部特性。Yule-Walker方法则是一种参数估计方法，用于估计自回归模型的系数。 4. **默示有效性**：论文证明了提出的估计量在特定假设下对误差分位数默示有效，意味着它能捕捉到误差的真实特性。 5. **渐近正态性**：作者表明，这个估计量的渐近分布与真实误差分位数相同，这是统计推断中的重要性质，因为它保证了估计的稳定性。 6. **预测区间构建**：基于误差分位数的估计，文章构建了AR(p)模型的预测区间。这样的预测区间在实际应用中非常有用，因为它们提供了对未来的置信范围。 7. **统计置信水平**：论文证明了构建的预测区间能渐近达到预定的置信水平，这意味着随着时间序列长度的增加，预测区间将更准确地包含未来观测值。 8. **模拟研究与实证分析**：为了验证理论结果，作者进行了大量的数据模拟实验，并将这种方法应用于实际数据，展示了其在实践中的适用性和有效性。 这些知识点对于理解时间序列分析，特别是在估计和预测AR(p)模型的误差特性和不确定性时，具有重要的理论和实践价值。