详解EM算法：理论与实例解析

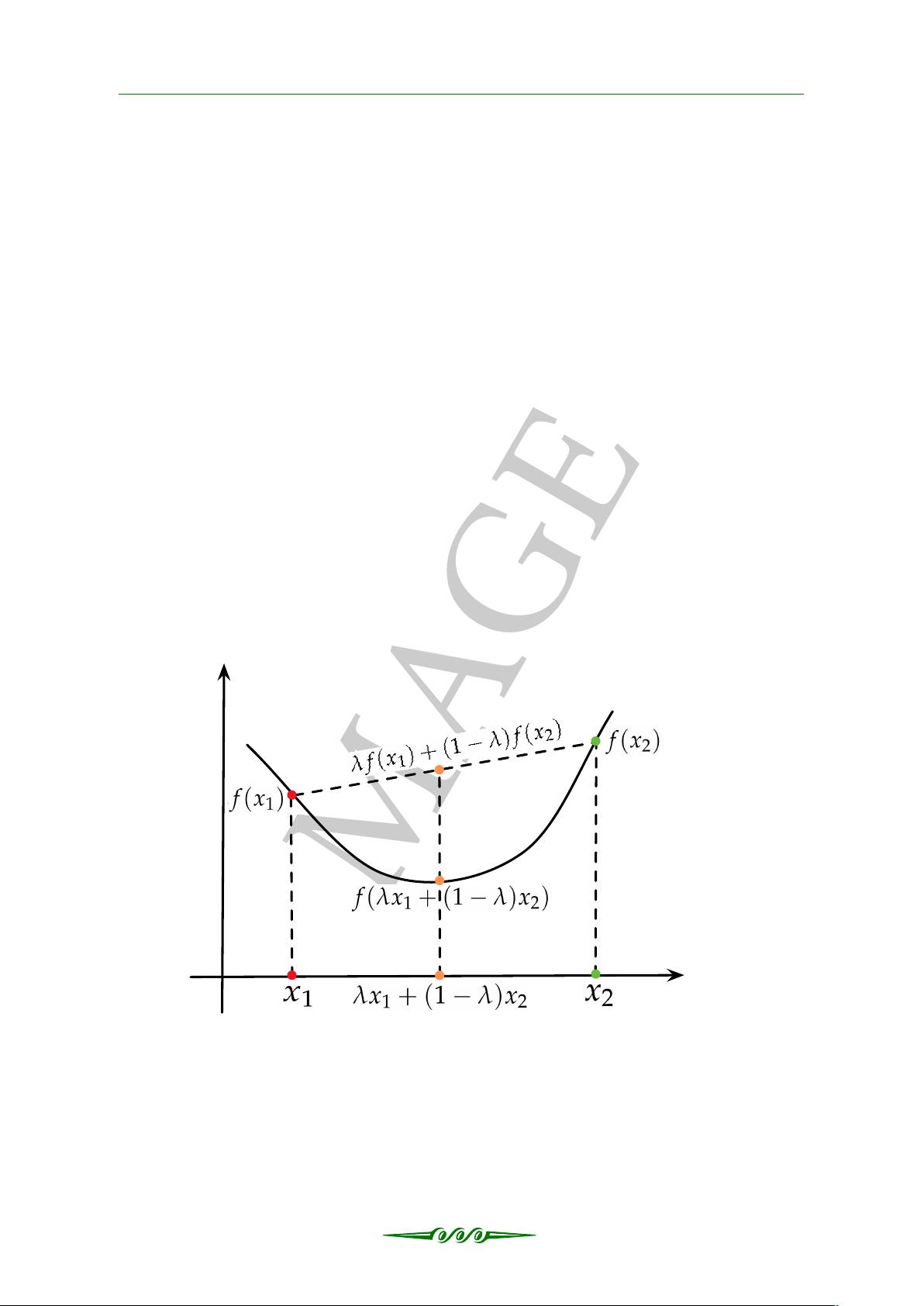
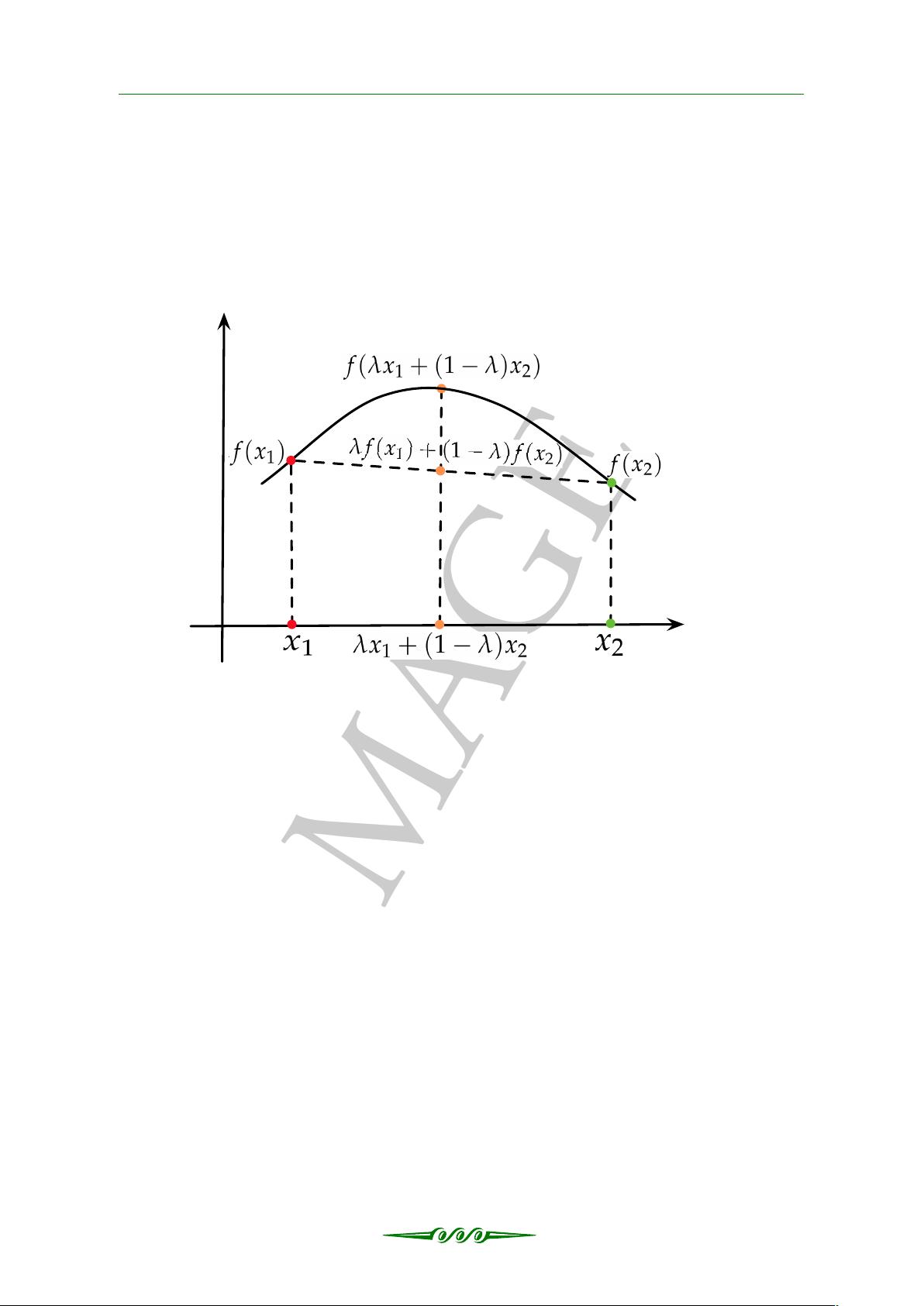
期望最大化算法(EM)是一种常用的无监督或半监督学习方法，特别适用于处理带有隐变量的数据集，比如在混合高斯分布、贝叶斯网络和因子分析等概率模型中。EM算法的核心思想是通过迭代的方式，交替优化观测数据的参数估计和隐变量的后验分布，即使在数据中存在缺失值或部分观察时也能进行有效的参数估计。 1. 基础知识准备： - **数学期望**：是随机变量的平均值，它表示一个随机变量取所有可能值的加权平均，对于EM算法来说，这是计算参数估计的重要工具。 - **极大似然估计**：是根据给定观测数据寻找模型参数的一种方法，目标是使数据的似然函数最大化的估计。在EM算法中，极大似然估计用于初始化和每次迭代后更新模型参数。 2. 凸函数与凹函数：在优化理论中，凸函数具有重要的性质，它的图形总是向上凸起，而凹函数则是向下凹陷。理解这些概念有助于理解EM算法中的梯度上升过程，因为优化目标通常是凸函数，从而保证了全局最优解的存在。 3. **詹森不等式**：这个不等式是衡量偏导数与原函数之间关系的一个工具，对于证明EM算法的收敛性和性能有着关键作用。在算法迭代过程中，利用詹森不等式可以确保每个步骤都在朝着增加总体似然的方向推进。 1.2 期望最大化算法理论推导： - **三枚硬币问题**：这是一个直观的示例，用于解释EM算法的基本运作。设想有三枚硬币，其中两枚公平，一枚偏斜。目标是估计每枚硬币出现正面的概率。在EM算法中，隐变量可能是硬币的种类，我们先用极大似然估计初始参数，然后通过迭代过程估计隐藏的硬币类型分布，同时更新各硬币的抛掷概率。这个过程直到达到局部最优或者满足停止条件。 通过三枚硬币问题的推导，我们可以看到EM算法的主要步骤：(1)初始化观测数据的似然函数；(2)用当前的参数估计隐变量的分布；(3)基于新的隐变量分布更新观测数据的参数；(4)重复步骤2和3，直至收敛。每一步都遵循数学期望和极大似然原则，确保模型参数逐渐接近真实分布。 总结来说，期望最大化算法是一种强大的工具，尤其适用于复杂模型中的参数估计。理解其背后的数学原理和关键概念如数学期望、极大似然、凸函数等，能帮助我们更深入地掌握这一方法，并在实际问题中有效地应用。同时，通过具体案例如三枚硬币问题，我们能看到算法的具体操作流程及其在优化过程中的应用。