深入理解B+、B-树及其平衡算法

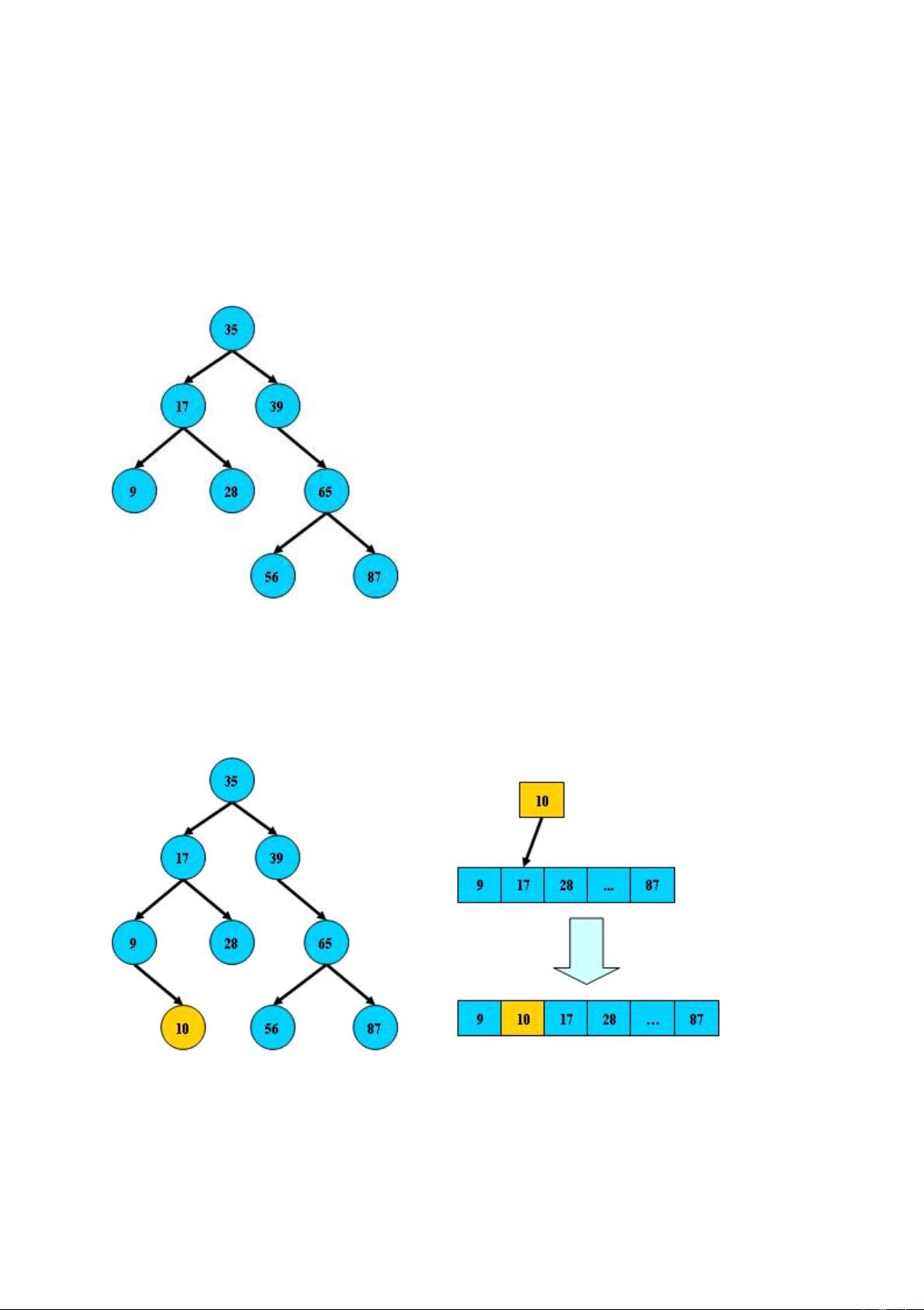
B+树、B-树、B树和B*树是数据结构中的关键元素，尤其在数据库管理系统中起着至关重要的作用。它们都属于多路搜索树，旨在提供高效的查找、插入和删除操作，同时保持数据的组织和存储效率。 B树是一种基本的多路搜索树，它遵循以下规则： 1. 所有非叶子节点最多有两个子节点，分别称为左（Left）和右（Right）。 2. 每个节点存储一个关键字，并按照关键字大小排序。 3. 非叶子节点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树。 4. B树的搜索过程类似于二分查找，通过比较关键字确定是继续向左还是向右。 然而，B树在处理大量数据时可能会导致不平衡，影响性能。为解决这个问题，B-树引入了改进。B-树允许每个非叶子节点具有多个子节点（M > 2），并且有特定的子节点数量限制。根节点的子节点数在[2, M]之间，而其他非叶子节点的子节点数在[M/2, M]范围内。每个节点至少存储M/2-1个关键字，并且保证这些关键字有序。 B-树的关键特性包括： 1. 所有叶子节点位于同一层，这有助于减少磁盘I/O操作。 2. 非叶子节点的关键字和指针数量根据子节点数进行调整，以保持平衡。 3. 在搜索过程中，对节点内有序的关键字进行二分查找，确保快速定位。 B+树是对B树的进一步优化，它将所有数据存储在叶子节点，而非叶节点只用于存储索引信息。这样，读取数据时几乎不涉及非叶子节点，提高了随机访问性能。B+树在数据库设计中常见于文件系统和大型数据库中，因为其支持高效的范围查询。 总结来说，B树、B-树和B+树都是平衡的数据结构，它们通过调整节点和子节点的数量，以及关键字的分布来维持数据的组织，从而提供高效的数据操作。在实际应用中，选择合适的树结构取决于具体的需求，如频繁的读取、写入操作以及对存储和查找性能的要求。在维护数据平衡的同时，也需考虑插入和删除操作的复杂性，以及平衡算法的设计。