算法导论第三版精选解答:排序与二分查找解析
需积分: 25 82 浏览量
更新于2024-07-25
收藏 420KB PDF 举报
"算法导论第三版的部分答案展示"
在《算法导论》第三版中,我们探讨了各种算法的设计和分析。以下是一些章节的解答摘要:
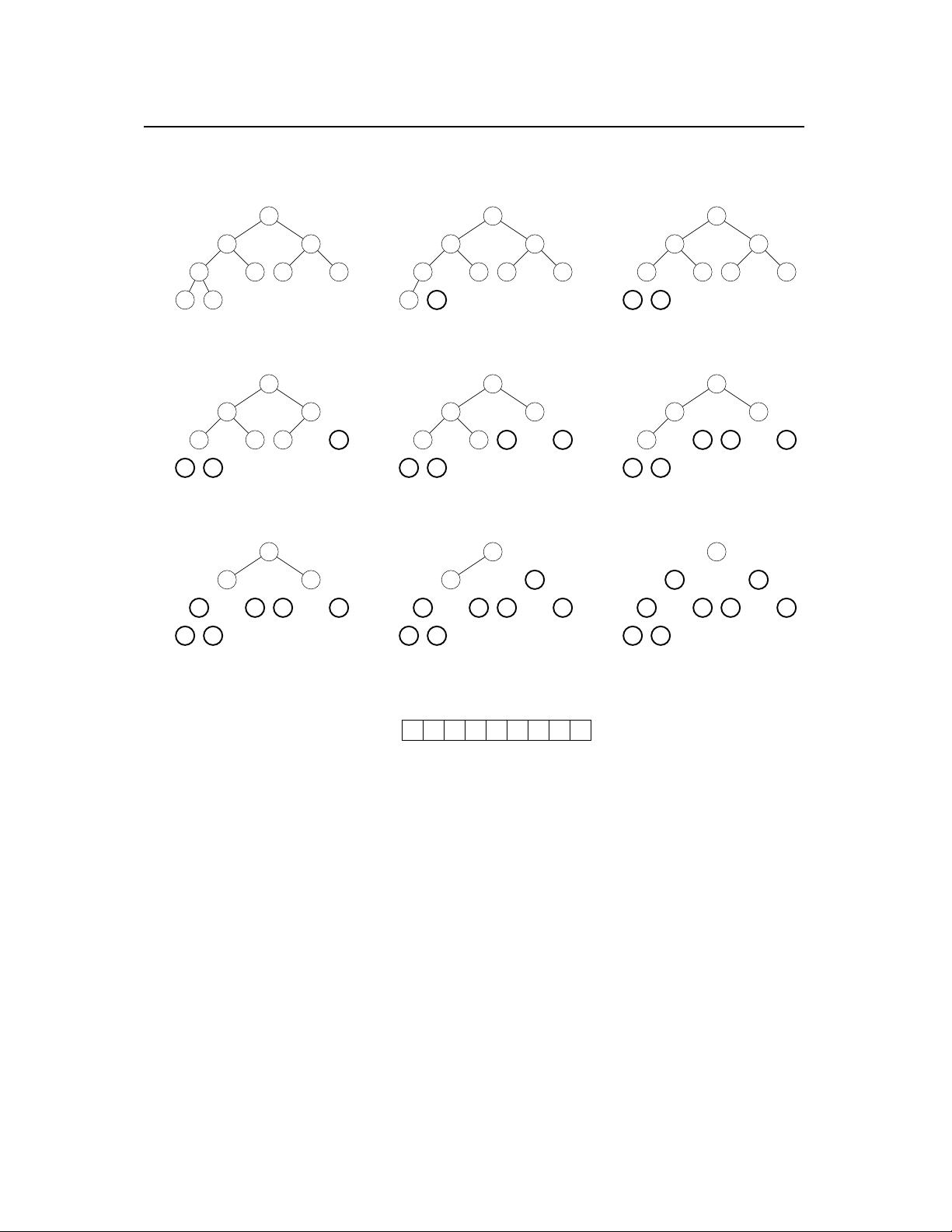
2.2章主要介绍算法的基础,其中Exercise 2.2-2讨论的是选择排序(Selection-Sort)算法。选择排序是一种简单直观的排序算法,它的基本思想是在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。算法的核心是一个嵌套的双层循环,外层循环控制排序的轮数,内层循环用于找到当前子数组中的最小元素并进行交换。这个算法保证了在每一轮迭代的开始时,前j个元素是原数组中最小的j个元素,并且这些元素已经排序好。当外层循环执行完n-1次后,整个数组就会被排序。选择排序的时间复杂度在所有情况下都是O(n^2)。
Exercise 2.2-4提出一个问题,即修改算法以检查输入是否满足特殊条件,并在满足时输出预计算的答案。这涉及到算法的最优情况运行时间,通常最优情况下的运行时间并不足以全面评估一个算法的效率,因为实际应用中我们更关心平均情况或最坏情况的性能。
2.3章则关注二分查找(Binary-Search)算法。二分查找适用于有序数组,它通过比较中间元素来缩小搜索范围。在给定的数组范围[low, high]中,如果目标值()等于中间元素,那么查找结束;如果目标值小于中间元素,则在左半部分数组[low, mid - 1]中继续查找;反之,在右半部分[mid + 1, high]中查找。每次比较后,搜索范围都会减半,直到找到目标值或搜索范围为空。二分查找的效率高,其时间复杂度为O(log n)。
这些解答为我们展示了算法设计的基本原则,包括如何优化算法以适应特定输入,以及如何通过循环和递归等结构实现排序和查找操作。在学习《算法导论》时,深入理解这些问题及其解答对于提高算法分析和设计能力至关重要。
1993 浏览量
311 浏览量
539 浏览量
339 浏览量
228 浏览量
186 浏览量
542 浏览量