布尔代数：逻辑门与二进制数据处理

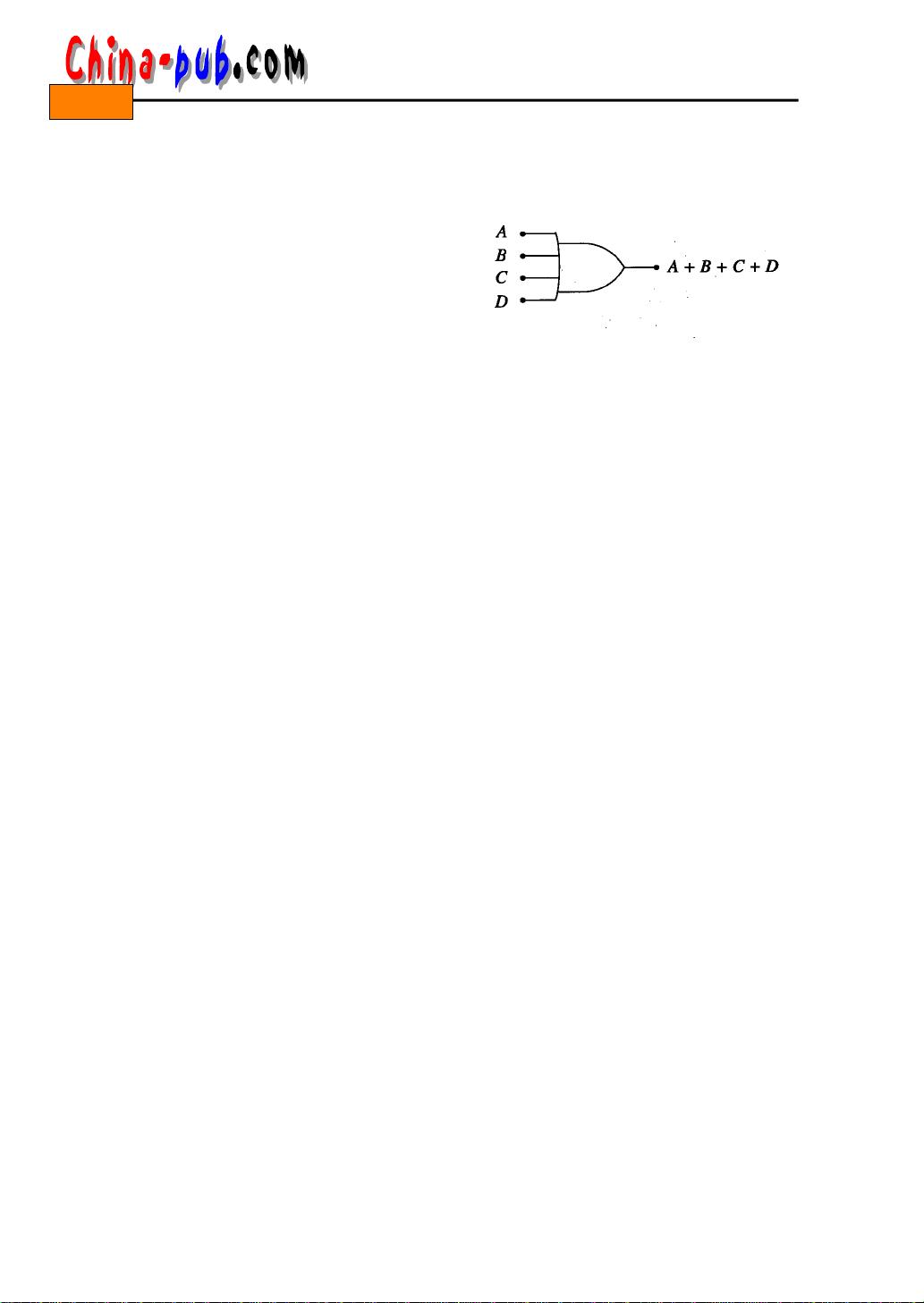
"布尔代数和逻辑门在数字计算中的应用，主要涉及二进制数制系统，是理解和设计现代电子电路的基础。" 布尔代数，源于19世纪数学家乔治·布尔的研究，是一种特殊的代数结构，专门用于处理二进制变量，即只有两个状态（0和1）的变量。这种代数理论在数字逻辑中至关重要，因为它提供了描述和分析二进制逻辑操作的框架。 在二进制数制系统中，数据的表示和处理是通过二进制位（bits）进行的。一个bit可以是0或1，代表两种可能的状态。为了表示更复杂的信息，我们可以使用多个二进制位组成一个二进制字，比如一个4-bit的二进制字可以有16种不同的组合，每种组合代表不同的数值或状态。这种组合方式使得二进制系统能够表示多种可能的值，而不仅仅局限于两个。 在数据处理层面，布尔代数的应用体现在逻辑门上。逻辑门是电子电路的基本单元，它们接收二进制输入（0或1），根据特定的逻辑运算规则产生一个二进制输出。常见的逻辑门包括AND门、OR门、NOT门（也称为反相器）以及更复杂的如NAND、NOR和XOR门。这些门电路的输出是基于输入变量的逻辑关系，例如AND门只有当所有输入都是1时才输出1，OR门只要有至少一个输入是1就输出1，而NOT门则反转输入的值。 逻辑门的组合可以构建出更复杂的逻辑函数，这些函数可以通过真值表来描述，列出所有可能的输入组合及其对应的输出结果。例如，一个三输入的逻辑函数f(A, B, C)的真值表将包括8行（因为有2^3种可能的输入组合），每行对应一个输入组合和对应的输出f。 布尔代数的运算规则，如合并律（A + (B + C) = (A + B) + C）、分配律（A × (B + C) = A × B + A × C）和德摩根定律（NOT(A AND B) = NOT A OR NOT B），在电路设计中有着广泛的应用，帮助设计者简化逻辑表达式，优化电路性能，减少所需的硬件元件数量。 在现代计算机科学和电子工程中，布尔代数和逻辑门构成了数字逻辑的基础，不仅应用于微处理器的设计，还影响着存储器、接口电路、计算机网络以及其他各种数字设备的开发。通过对布尔代数的深入理解和掌握，工程师能够设计出高效、可靠的数字系统，推动信息技术的发展。