Mathematica：多项式运算与方程求解详解

Mathematica是一款强大的数学计算软件，它在处理多项式运算上表现出色，提供了多种功能来简化复杂的数学表达式。本文将详细介绍Mathematica中关于多项式操作的一些关键功能和实例。 首先，多项式在Mathematica中被视为一种特殊的表达式，其运算遵循表达式的一般规则。软件内置了一组函数，如： 1. `Expand`函数用于按幂次展开多项式，如`Expand[poly]`用于一般展开，`ExpandAll[poly]`则进行全部展开。 2. `Factor`函数用于因式分解多项式，`Factor[ploy]`进行整体分解，`FactorTerms[ploy, {x, y,...}]`按指定变量分解。 3. `Simplify`和`FullSimplify`用于将多项式化简至最简形式，前者默认处理，后者先展开再简化。 4. `Collect`函数则根据指定变量展开多项式，如`Collect[poly, x]`按x的幂次展开，`Collect[poly, {x, y,...}]`按多个变量展开。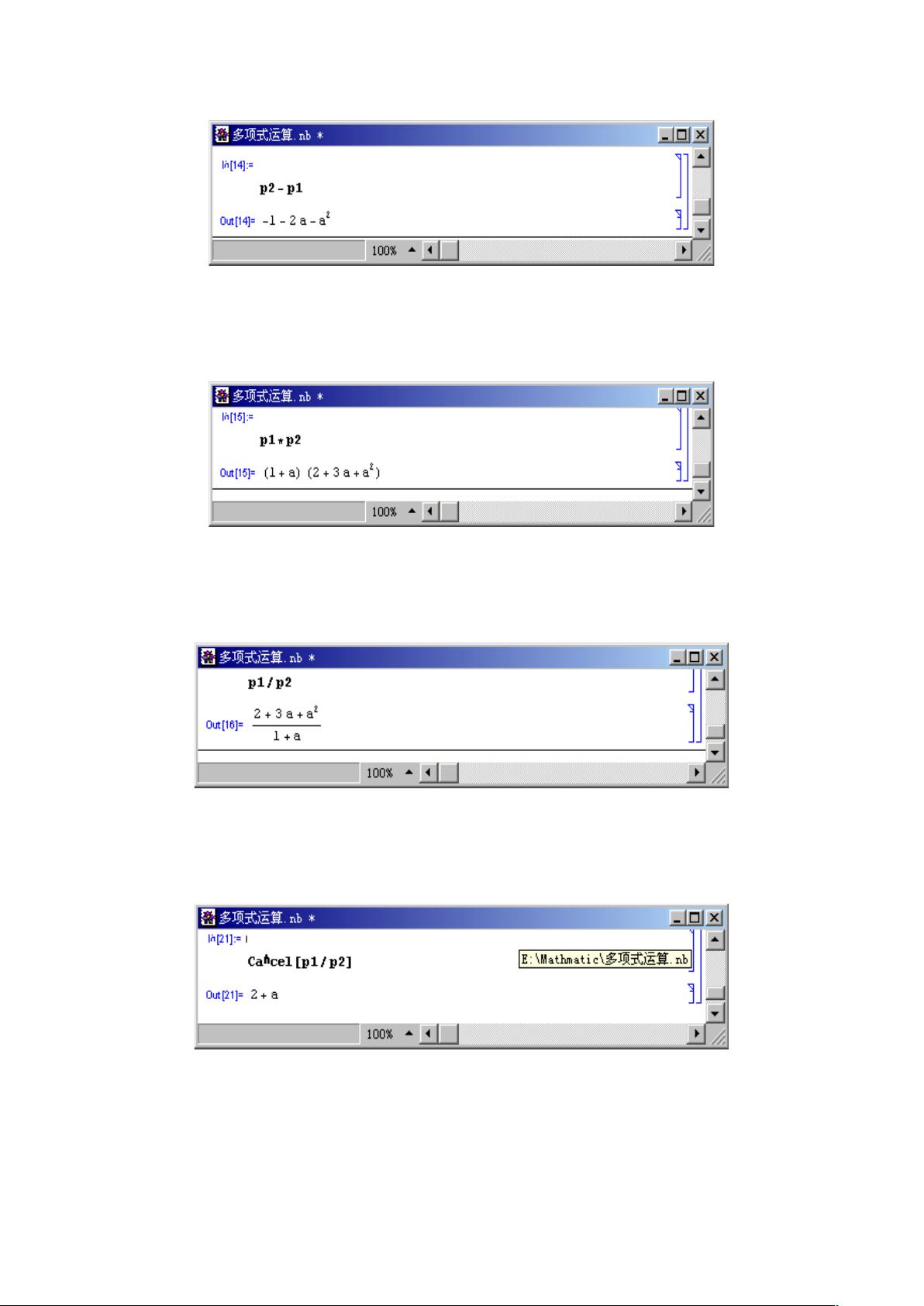 例如，对多项式`x^8 - 1`的因式分解和多项式`(1 + x)^5`的展开，Mathematica提供了直观的图形输出。此外，还展示了多项式的加减乘除运算，如将多项式`a^2 + 3a + 2`和`a + 1`相加，以及使用`Cancel`函数去除公因式。对于多项式除法，`PolynomialQuotient`和`PolynomialRemainder`函数分别返回商式和余式。 方程求解也是Mathematica的强大功能之一。软件将方程视为逻辑语句，使用双等号`==`表示逻辑等价，而非赋值。例如，求解`x^2 - 3x + 2 = 0`的根，可以使用`Roots`得到根的表示形式，而`Solve[]`则返回解集。一元代数方程的求解同样方便快捷，能够高效地处理复杂的数学问题。 通过这些函数和操作，Mathematica为用户提供了强大的工具，使得处理多项式运算变得简单且精确。无论是基础的多项式操作还是高级的方程求解，都能在Mathematica中找到解决方案，适用于科学研究、数据分析和教学等多个领域。