柯西不等式：重要性质与应用详解

柯西不等式，又名Cauchy-Buniakowsky-Schwarz不等式，是数学分析中的一个基本不等式，由法国数学家奥古斯丁-路易·柯西首次提出，但在积分学中得到了进一步发展和完善。这个不等式的重要性在于其广泛的应用价值，能够帮助解决诸如证明不等式、解三角形、求函数最值以及处理方程等问题。 二维形式的柯西不等式表达为：对于实数a, b, c, d，有(a² + b²)(c² + d²) ≥ (ac + bd)²。当且仅当ad = bc时，等号成立。这个形式直观地展示了内积的性质，即向量的平方和乘以其对应的点积的平方，总是大于等于点积的平方。 三角形式则涉及到向量的模长，即√(a² + b²) + √(c² + d²) ≥ √[(a + c)² + (b + d)²]，同样在ad = bc时达到等号。这个版本强调了线性代数中向量长度的几何意义。 向量形式的柯西不等式更通用，适用于n维空间，对于向量α=(a1, a2, ..., an)和β=(b1, b2, ..., bn)，有|α||β| ≥ |α·β|，其中"·"表示内积，等号成立条件是β为零向量或α与β共线。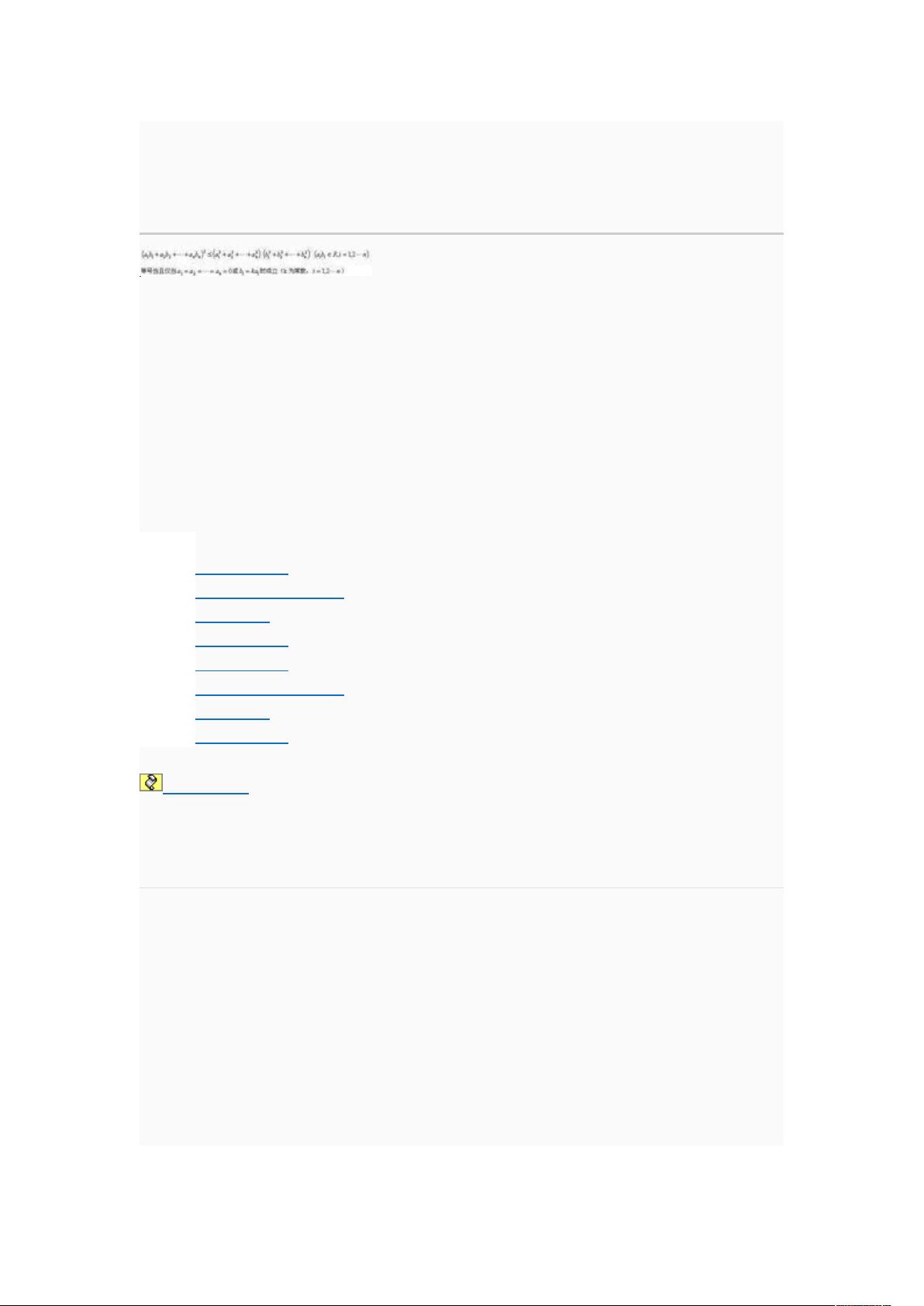 一般形式的柯西不等式为：对任何实数序列{ai}和{bi}，有(∑ai²)(∑bi²) ≥ (∑ai·bi)²，等号成立当且仅当ai/bi在整个序列上恒定，或者ai和bi中有至少一项为零。 推广形式，也被称为卡尔松不等式，适用于多变量情况，如在m×n矩阵中，各行元素的几何平均数乘积不小于相应列元素的几何平均数乘积的几何平均数。这体现了不等式的扩展性和在多元数学中的应用。 柯西不等式的证明通常涉及代数运算和展开，例如，二维形式通过展开并重新组合项来展示其有效性。证明过程可能利用到多项式的平方和展开，以及向量和内积的性质。 柯西不等式不仅是理论研究的重要工具，也是实际问题求解中的有力武器，其广泛应用在微积分、线性代数、概率论、统计学以及物理学等领域。掌握这个不等式及其各种形式，对于深入理解数学分析和应用数学具有重要意义。