《信息论与编码》笔记——香农熵、信道容量与编码
需积分: 0 22 浏览量
更新于2024-06-18
收藏 2.14MB PDF 举报
该笔记是基于《信息论与编码》(电子工业出版社)编写的,涵盖了信息论的基础概念和重要理论,包括信息的定义、信源与熵、信道及其容量、无失真信源编码和信道纠错编码等内容。
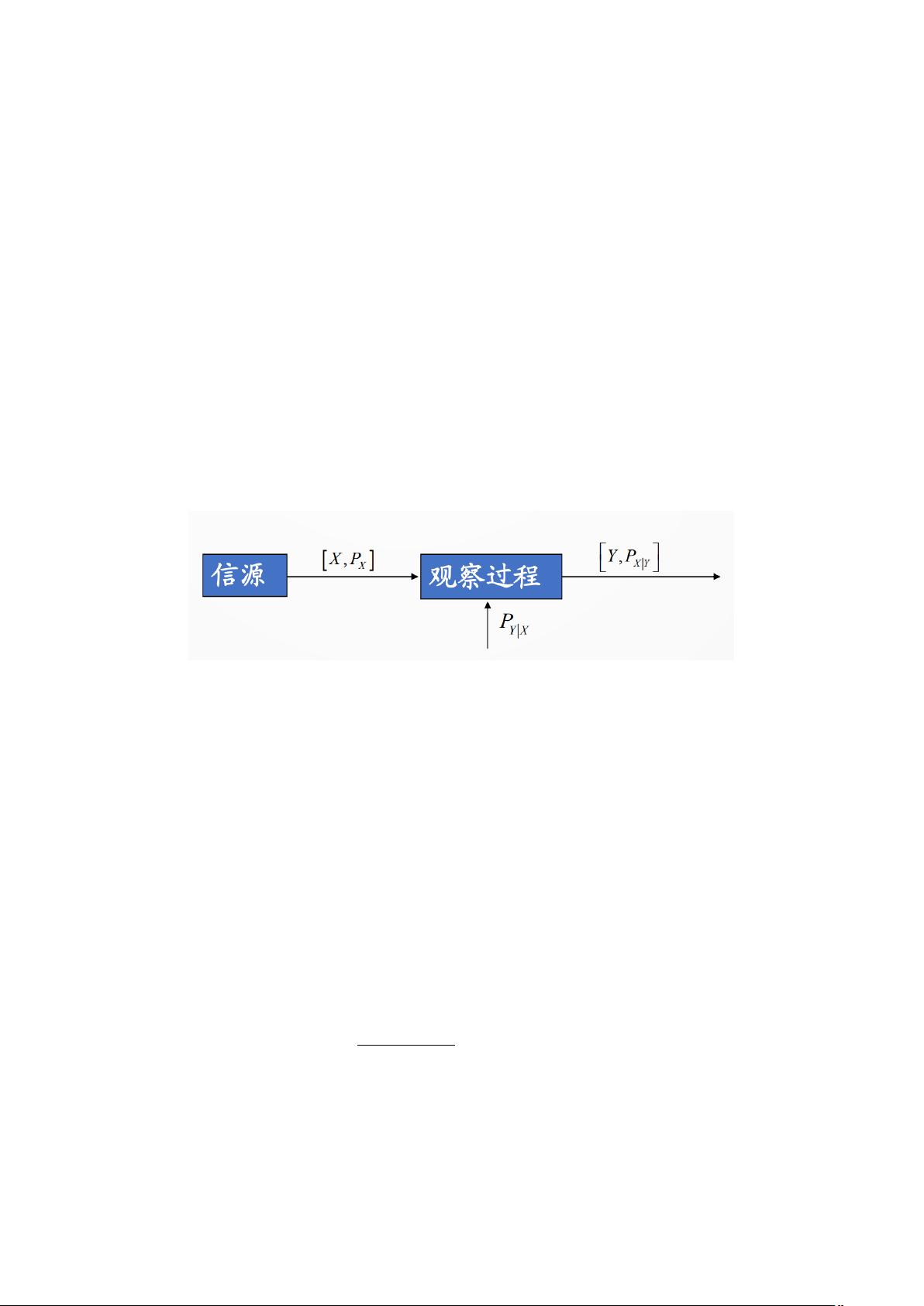
1. 信息的定义
信息论起源于1948年香农的开创性工作,他将信息定义为不确定性的减少。在这个框架下,信息量与事件的不确定性成正比,而不确定性可以用概率来度量。先验概率P(X)表示在没有观察Y时对X的不确定性,后验概率P(X|Y)则是在观察到Y之后对X的不确定性。信息量可以被看作是这两者之间的差值,即先验不确定性减去后验不确定性。
2. 信源与熵
- 香农熵:是衡量随机变量不确定性的度量,对于离散信源,熵H(X)定义为所有可能消息出现概率的加权平均的负对数。它反映了信源发出消息的平均信息量。
- 联合熵H(X,Y)描述两个随机变量X和Y的不确定性,而条件熵H(X|Y)表示在已知Y的情况下X的不确定性。
- 平均互信息量I(X;Y)衡量了两个随机变量之间的关联程度,它是H(X)和H(X|Y)的差,表示从Y中获取信息对X不确定性的影响。
3. 信道及其容量
- 信道的基本参数包括输入、输出、传输概率和噪声特性。
- 对于离散 memoryless channel (DMC),信道容量C是最大可能的平均互信息量,表示在无错误传输条件下,信道能传输的最大信息速率。
- 连续信道的信道容量涉及高斯分布和信噪比的概念,通常需要更复杂的分析来确定。
- 波形信道和连续信道的容量讨论了模拟信号传输的限制和优化策略。
4. 无失真信源编码
- 信源编码旨在用尽可能少的比特来表示信源输出,同时保证解码后的信息无损。
- 基本概念包括编码的唯一可译性,确保编码和解码的一致性。
- 定长编码和变长编码定理阐述了无失真编码的理论界限,如哈夫曼编码、算术编码和游程编码是常见的无失真编码方法。
5. 信道纠错编码
- 信道纠错编码是为了应对信道引入的错误,通过在原始信息中添加冗余信息来检测和纠正错误。
- 常见的纠错编码有奇偶校验、汉明码、卷积码和涡轮码等,它们在不同的应用场景中提供不同程度的错误保护能力。
本笔记不仅提供了信息论的基础知识,还强调了这些理论在实际通信系统中的应用,旨在提升信息传输的效率、可靠性及安全性。
4481 浏览量
663 浏览量
713 浏览量
1787 浏览量
526 浏览量