分治法解决最近点对问题

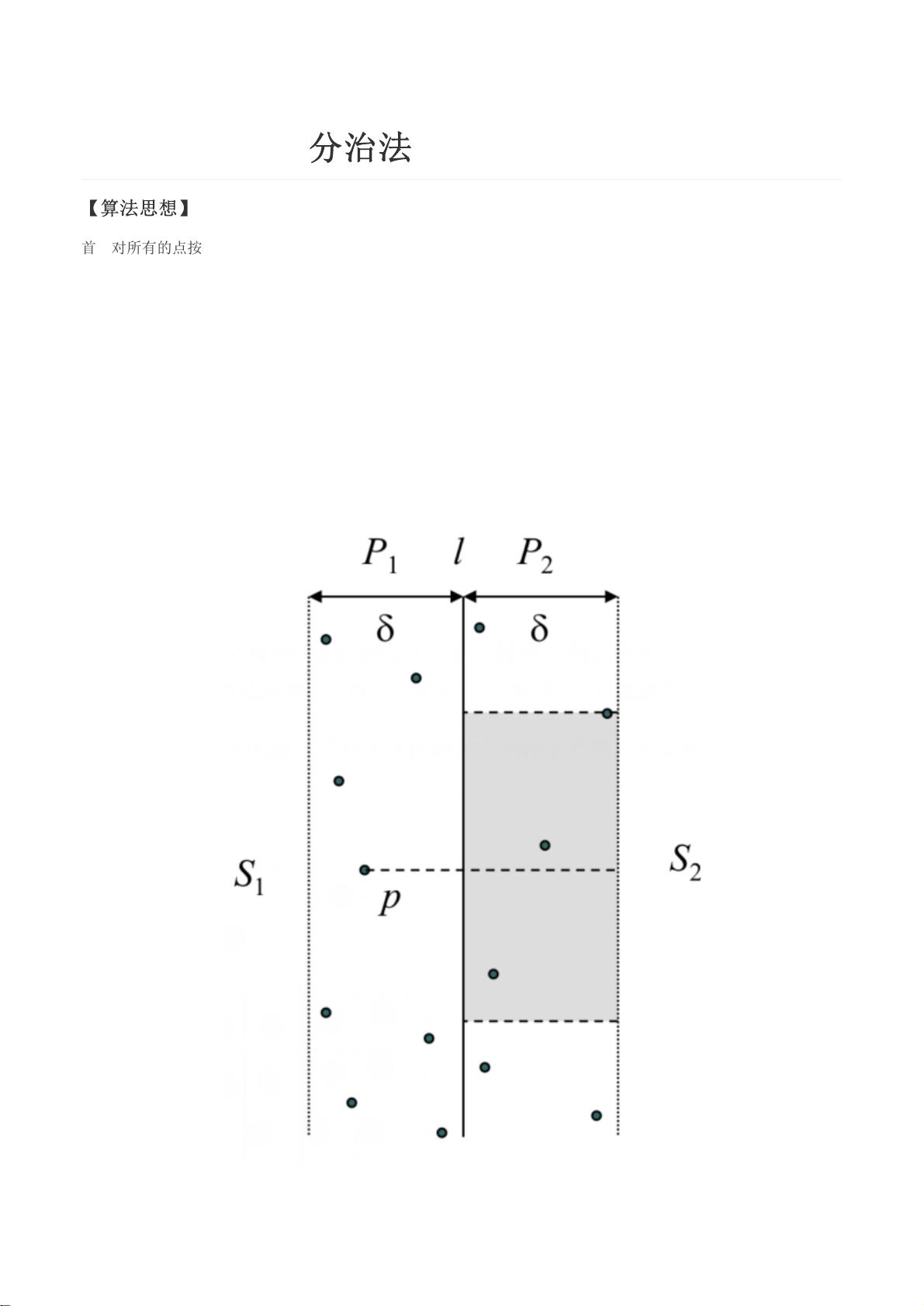
"Closest Pair 分治法算法的实现与解析" Closest Pair问题是一个经典的计算机科学中的几何算法问题，其目标是在二维平面上的一组点中找到最近的两点对。这里的分治法策略是一种有效的解决方法，它可以将大问题分解成小问题，逐层递归地解决，最后合并结果。 算法思路如下： 1. **预处理**：首先对所有点按照x坐标进行排序。这样可以确保在后续处理过程中，点总是按照x坐标顺序排列。 2. **分割**：使用二分法将排序后的点集分成两部分，直到每部分包含2或3个点。这是因为当点的数量非常少时，我们可以直接计算所有可能的点对组合，找出最近的点对。 3. **子问题处理**：对于每个子问题，我们需要检查子问题边界附近的点与另一子问题中所有点的距离。但是，我们不需要比较所有点对，而是只考虑那些距离子问题边界线小于当前已知最小距离(min_len)的点。 4. **优化**：避免不必要的计算。在x轴上，我们只需要考虑那些离边界线小于min_len的点。同时，如果我们在y轴上也进行排序，可以进一步减少需要检查的点的数量。例如，对于子问题S1中的点p，我们只需考虑那些在以p为中心，半径为min_len的圆内的点。为了简化，我们可以假设p位于边界线上，这样需要考虑的区域就是图中灰色部分所示。 5. **代码实现**：给出的代码定义了结构体`Record`用于存储最近点对的信息，结构体`Points`表示二维空间中的点，以及`dis()`函数来计算两点间的距离。此外，`min()`函数用于取两个数中的较小值，`cmpx()`和`cmpy()`是用于排序的比较函数。 6. **递归终止条件**：当子问题规模减小到2或3个点时，可以直接计算这些点之间的距离，找出最近的点对。 7. **合并结果**：在递归的每一层，都会找到两个子问题内的最近点对。最后，需要将这些结果进行比较，找出全局的最近点对。 通过这种分治策略，算法的时间复杂度可以达到O(n log n)，比简单的O(n^2)算法有了显著的改进。在实际应用中，这种优化对于大数据集来说至关重要，因为它大大减少了计算量。