数字信号处理：基2 FFT算法实现与扩展

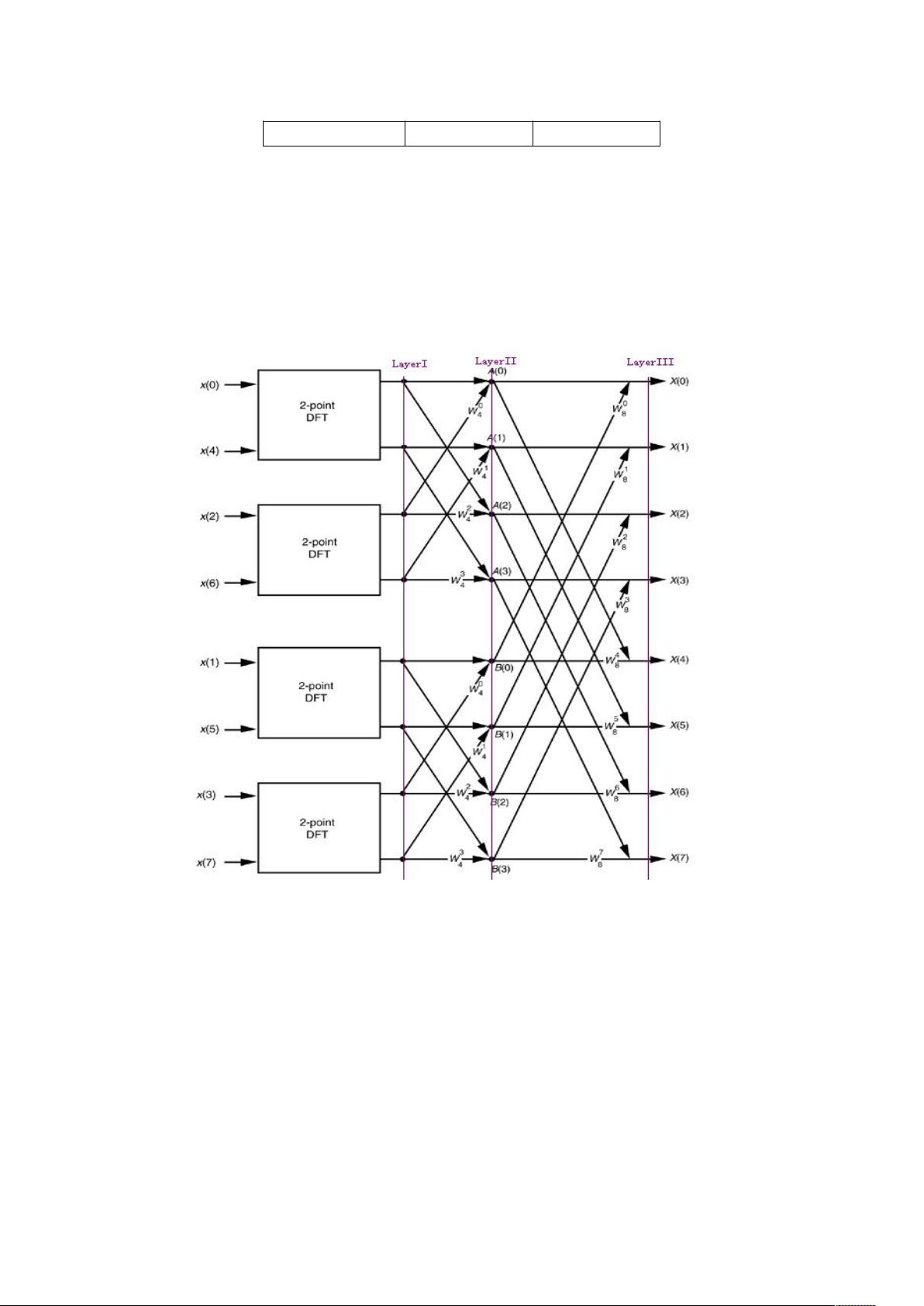
"FFT基2 FFT编程涉及到快速傅里叶变换（FFT）的实现，特别是针对8点序列的基2-DIT-FFT或基2-DIF-FFT算法。该编程任务旨在通过Matlab或C语言等实现，并可以扩展到用户自定义的2的幂次点数。设计目标是理解和掌握FFT在数字信号处理中的重要性，以及通过快速算法减少计算复杂度。本文将详细介绍基2 FFT的工作原理，并提供一个简单的2点FFT伪代码示例。 FFT（快速傅里叶变换）是离散傅里叶变换（DFT）的一种高效算法，主要解决DFT计算量大的问题。在通信、图像处理、雷达等领域，DFT的频谱分析是至关重要的。然而，原始的DFT计算复杂度为O(N^2)，对于大规模数据处理难以实现实时计算。FFT算法将这个问题的复杂度降低到O(N log N)，大大提高了计算效率。 基2 FFT算法通常分为两种类型：按时间抽取的DIT（Decimation In Time）和DIF（Decimation In Frequency）。这两种方法都涉及将输入序列分解为偶数和奇数部分，然后递归地计算更小的DFT。对于8点序列，首先根据n的奇偶性进行分组，然后分别计算两部分的DFT。接着，使用特定的旋转因子（W系数）将这些较小的DFT组合成完整的N点DFT。 扩展到N>=8点，需要确保点数是2的幂，如果不足则通过加零补长。例如，若用户指定N=16，那么原有的8点算法会被应用于两组8点序列，每组再分解为4点，如此递归进行，直到每次处理的点数为2。 以下是一个简单的2点DFT的伪代码示例，演示了如何利用基2 FFT计算： ```c #define N 2 #define PI 3.1415926 int i, j for (i = 0; i < N; i++) { X[i] = 0.0; // 初始化输出序列 } for (i = 0; i < N; i++) { // 对输入序列进行循环 for (j = 0; j < N; j++) { // 应用DFT公式 X[j] += x[i] * cos(2 * PI * i * j / N); if (i != j) { // 如果i≠j，需要加上负的相位项 X[j] -= x[i] * sin(2 * PI * i * j / N); } } } ``` 以上伪代码展示了2点DFT的基本计算过程，实际的基2 FFT算法会包含更复杂的分治策略和W系数的应用，以适应更大的N值。 通过理解和实现FFT，不仅可以深化对数字信号处理的理解，还能提高处理大规模数据的能力，这对于现代科技领域的许多应用至关重要。完成这样的编程任务有助于开发者熟练掌握这种核心算法，从而在实际工程中有效地应用。