树状数组详解：高效修改与求和

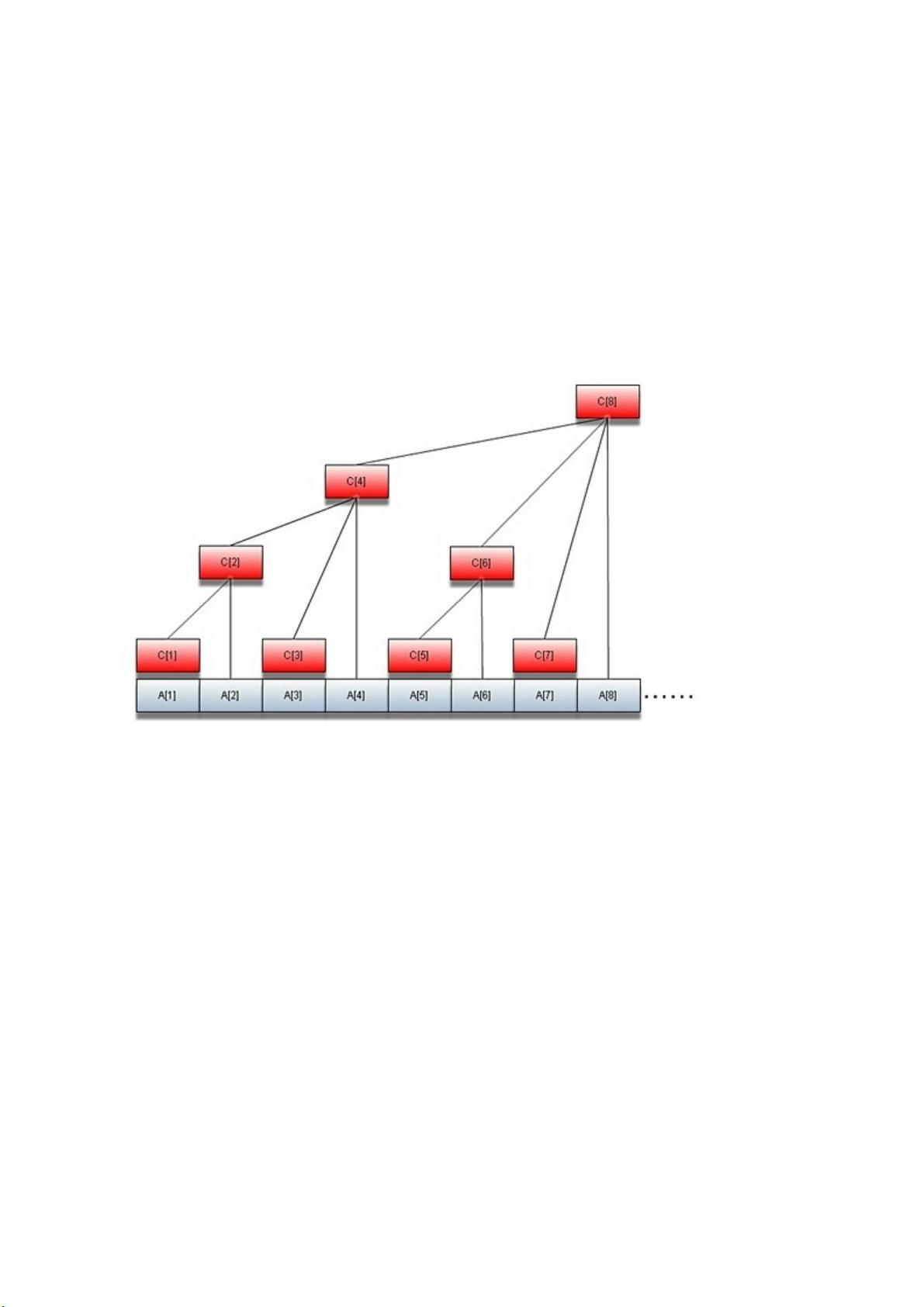
"这篇资源是关于树状数组的讲解，主要介绍了树状数组的基本概念、理论以及相关的操作，包括修改和求和操作的O(logn)时间复杂度，并提供了简单的C语言实现代码片段。" 树状数组是一种高效的数据结构，主要用于处理动态区间求和问题。在ACM算法竞赛中，这种数据结构常常被用来优化那些涉及到数组前缀和频繁修改的题目。传统的数组在修改一个元素后，需要重新计算受影响的所有前缀和，时间复杂度为O(n)。然而，树状数组通过一种特殊的数组结构和高效的更新策略，使得修改和查询操作的时间复杂度降低到O(logn)。 理论部分解释了树状数组的结构。树状数组C[]可以理解为一个数组的二进制表示，每个C[i]存储了从A[i-2^k+1]到A[i]的和，其中k是i的二进制表示中末尾0的个数。这样的设计使得树的高度不超过logn，从而保证了操作的效率。 修改操作：当需要修改A[i]时，从C[i]开始，向上逐级更新其所有祖先节点（即对应2的幂的子树的和），直到根节点。父节点的下标可以通过i + 2^k得到，其中2^k是i的二进制表示中最小的幂，即i^(i^(i-1))。 求和操作：查询前n项和，需要找到n之前的最大子树的根节点，将它们的C值累加。每个子树的大小为2的幂，可以通过减去2的最小幂找到前一棵子树，即p = i - i^(i^(i-1))。 代码片段包括两个函数：`intLowbit(int t)`用于计算t的最低位1对应的2的幂，这是找到子树规模的关键；另一个是`求前n项和`的部分，虽然这里没有提供完整的代码，但通常会涉及递归或迭代的过程，根据低bit信息进行查询。 树状数组的实现需要注意位运算的巧妙运用，这使得它在处理大规模数据时表现出色。学习和掌握树状数组对于提升动态区间查询的算法能力至关重要。在实际应用中，除了基础的修改和求和，还可以扩展到更复杂的区间操作，如区间加法、区间最值查询等。