没有合适的资源?快使用搜索试试~ 我知道了~
首页数学建模与传染病疫情分析
数学建模与传染病疫情分析
需积分: 46 39 下载量 101 浏览量
更新于2023-03-03
6
收藏 258KB PDF 举报
数学建模是一门比较有用的学科,如何学习好数学建模并应用到生活中是人们比较关注的;本文结合传染病疫情介绍了数学建模在现实生活中的应用。
资源详情
资源推荐

1
数学建模与传染病疫情分析
数学建模与传染病疫情分析
数学建模与传染病疫情分析
数学建模与传染病疫情分析
摘要
传染病是由各种病原体引起的能在人与人、动物与动物或人与动物之间相互传播
的一类疾病 。 历史上 , 人类一直在不停的与各类疾病做斗争 , 从 14 世纪 , 流行于整个
亚洲 、 欧洲和非洲北部的 “ 黑死病 ” , 到西班牙大流感 、 英国的疯牛病 、 2001 年英国口
蹄疫 、 2003 年我国内地 24 个省区市先后发生非典型肺炎疫情 ( SARS ) 、 2004 年禽流感
,
到近日的墨西哥猪流感( H1N1 ) ,灾难一次次在人间上演。
传染病疫情的蔓延可分早 、 中 、 晚三期 , 早期受感染人数较少 , 其传播速度 、 疫情
范围都较小,此时采取积极有效措施可有效抑制疫情的扩散;假如措施不到位,没有
很好的抑制疫情 , 则受感染的人数将增大 , 发展到中期 , 此时受感染的人数快速增加
,
范围最广,会给社会和人们的生命带来巨大危害;而到后期,由于医学治疗及相关疫
苗的研制、部分患者死亡或康复,受感染的人数将持续下降,直至最终趋于零。传染
病疫情在各个时期的传播速度、受感染人数均不同,有明显的特点。本文结合当前流
行的甲型 H1N1 流感的特点,采用 AHP 层次分析法建立模型,并运用 2003 年发生的非
典型肺炎疫情( SARS )所记录的数据分析论证,得出最终结论。
接触性高危型传染病是经由近距离接触已被传染病人,或在病源存活时间内直接
接触受病源感染的物件才有可能感染。从疫情传播的实际情况出发,参考相关数据,
运用数学建模的方法,建立疫情防治的数学模型,并解决下列问题:
( 1 ) 对疫区受感染人口增加的中短期趋势进行预测 , 并指出模型中的优点和不足
之处;
( 2 ) 对疫区受感染人口增加的长期趋势进行预测 , 并指出模型中的优点和不足之
处。
关键词:数学建模
AHP
层次分析法 甲型
H1N1
流感

2
一、模型假设
( 1 ) 疫区人口基本保持不变;
( 2 ) 同一年龄的人有相同的感染机会和痊愈能力;
( 3 ) 假设首先发病者为境外移入;
( 4 ) 得病后多数病人会往医院医疗,进入医院后只有院内感染可能,院内感染
几率随疫情持续时期有不同;
二、符号说明
模型建立过程中使用的符号及其意义如表一所示。
表一、模型中使用的符号及意义
序号 符号 含义 备注
1 t 时间 天
2 M 某地区人口总数 人
3
0
V
初始病人数
4 V ( t ) t 时刻被感染的人数 人
5
k ,
'
k
比例常数,可根据发病
情况的统计数据来确定
6 S ( t ) t 时健康人数
三、模型的建立与求解
(一)问题的分析
在本模型里,我们主要解决的问题是对疫区受感染人口的增加趋势做一个中短期
预测 。 假设首先发病者为境外移入 , 人数为 , 以 V(t) 表示发现首例病人后 t 时刻被感
染的人数 , 则 M — V ( t ) 就表示此时刻未被感染的人数 。 在传染病流行的初期 , 由于 V
( t ) 较小 , 能接触到感染者的人数少 , 单位时间内内被感染的人数也较少 , 因而传播
速度较慢 ; 而在传染病流行的后期 , 由于大多数人已经被感染 ( V(t) 较大 ) , 未被感染
的人数 M — V ( t ) 已经不多 , 所以此时单位时间内被感染的人数也不多 , 因而传播速度
也很慢。排除上述两种极端的情况,当有很多的感染者和很多的未感染者时,传染病
的传播速度是很快的。因此,传染病的发病率一方面受感染人数的影响,另一方面也
受未感染人数的制约。
由于所考虑的地区人口数量基本稳定,故可视为闭区域,即设总人口为常数 M ,时
间单位以天记, t 时刻被感染的人数为 V ( t ) ,初始病人数为 V0 ,当 M 》 1 时,该离散
问题可用连续问题来近似处理。
(二)模型的建立
1 、模型 Ⅰ (指数模型)
假设每个病人单位时间内的传染率为常数 k ,则 [t , t+ △ t] 时段内病人的增加数为
△ V=V(t+ △ t)-V(t)=k V ( t ) △ t.
当 t → 0 时 , 得微分方程初值问题
0
(0)
dV
kV
dt
VV
=
=
………………①
其解为
0
()
kt
VtVe
=
该指数模型属于最简单的增长模型 , 即著名的 Malthus 模型 。 由于粗糙 , 模型 Ⅰ 在
3
早期进行预测时 , 与实际情况相接近 ; 而中 、 晚期估计则偏差较大 , 尤其是当 t →∞ 时
,
V ( t ) →∞ ,这种情况与实际不符。出现的这种情况的一个重要原因在于未考虑健康
人数的不断减少, k 为常数与实际不相符了。
2 、模型 Ⅱ ( SI 模型)
假设每个病人单位时间内传染人数与健康人数 S ( t ) 成正比 , 即
'
()
kkst
=
,
'
k
为
传染系数,且 ()t
VtSM
+= ( ) ,将
''
()k(())
kkstMVt
==− 代入式 ① 得
'
0
(())
(0)
dV
kMVtV
dt
VV
=−
=
得其解析解为
'
.
()
1(1)
kMt
M
Vt
ae
−
=
+−
,
0
M
a
V
= .
这就是著名的 Logistic 模型 , 可用来预报传染病高峰来临的时刻
1
t
, 曲线 ()
Vt
形
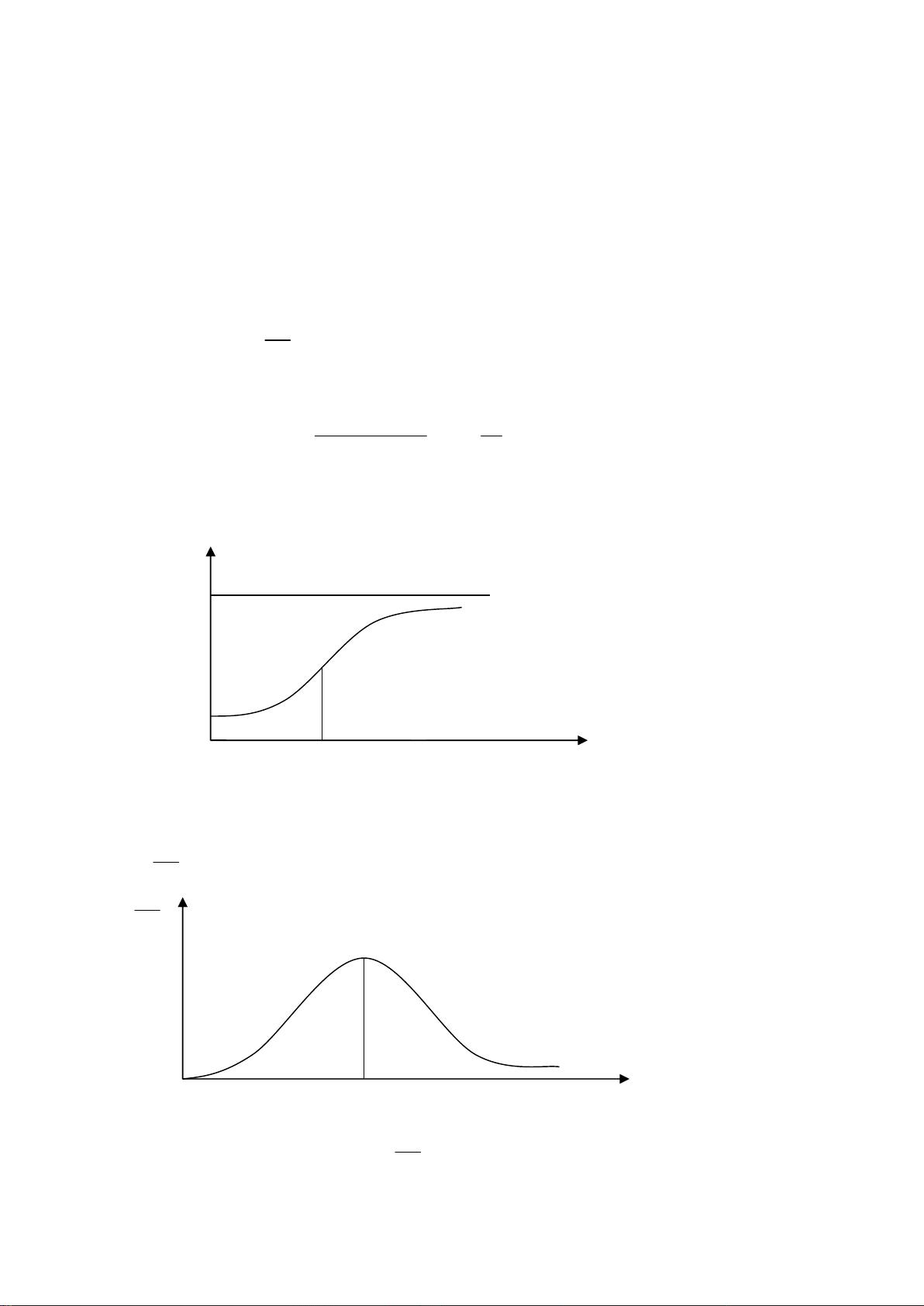
如 S 形,故常常称为 S 曲线;如图一所示。
()
Vt
M
0
V
0
1
t t
图一 Logistic 模型的 ()
Vt
-t 曲线
dV
dt
~ t 曲线表示了病人增长率与时间的关系,如图二所示。
d
V
dt
0
1
t t
图二 Logistic 模型的
dV
dt
~ t 曲线
剩余10页未读,继续阅读
安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功









