没有合适的资源？快使用搜索试试~ 我知道了~

首页Android Matrix理论与应用详解

Android Matrix理论与应用详解

Matrix

需积分: 10 74 浏览量更新于2023-03-03 评论收藏 534KB DOC 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

试读

12页

Android Matrix理论与应用详解Android Matrix理论与应用详解Android Matrix理论与应用详解Android Matrix理论与应用详解

资源详情

资源评论

资源推荐

Matrix 学习——基础知识

以前在线性代数中学习了矩阵，对矩阵的基本运算有一些了解，前段时间在使用 GDI+的时候再次学习如何使用矩阵来变

化图像，看了之后在这里总结说明。

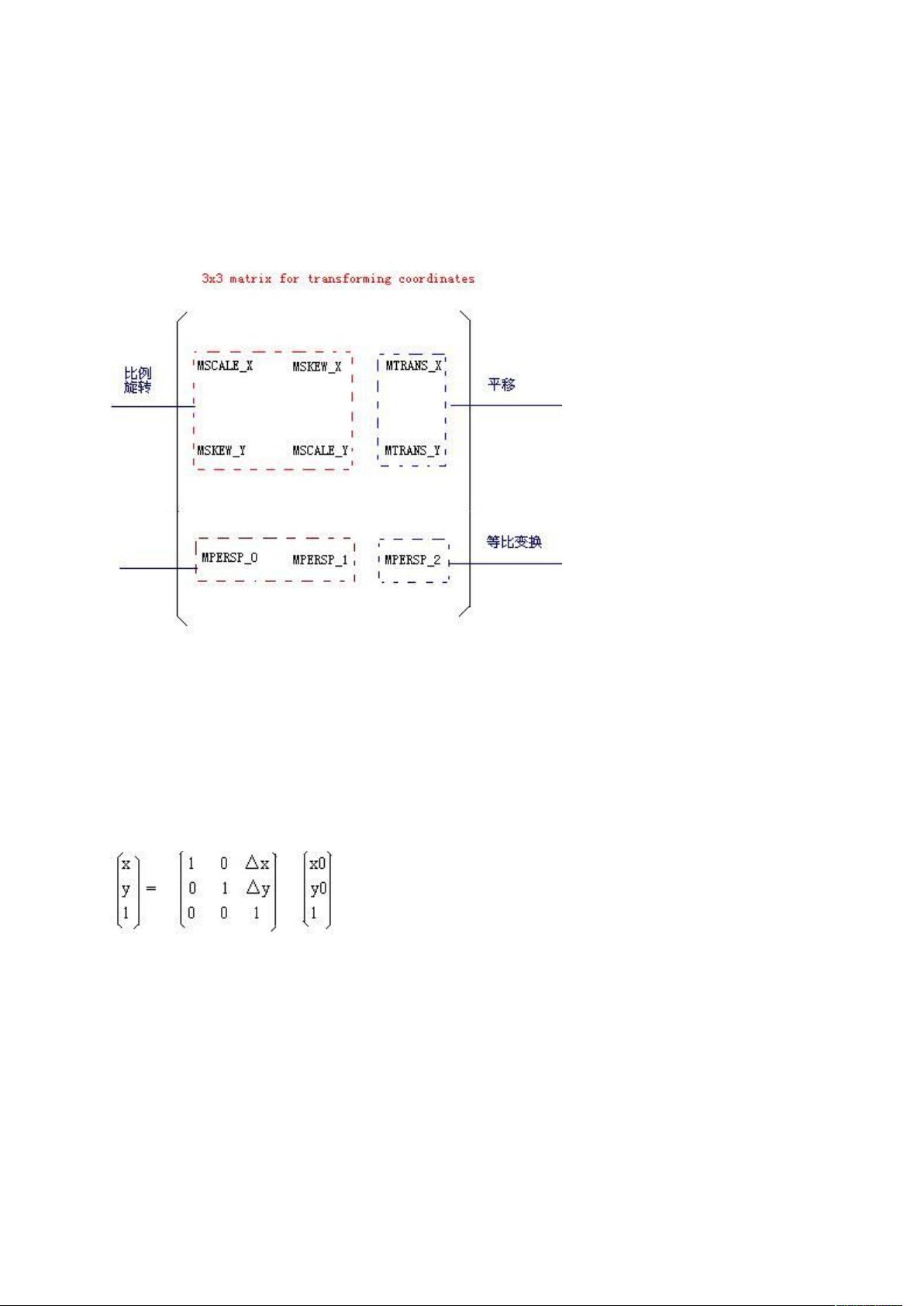
首先大家看看下面这个 3 x 3 的矩阵，这个矩阵被分割成 4 部分。为什么分割成 4 部分，在后面详细说明。

首先给大家举个简单的例子：现设点 P0（x0， y0）进行平移后，移到 P（x，y），其中 x 方向的平移量为△x，y 方向

的平移量为△y，那么，点 P（x，y）的坐标为：

x = x0 + △x

y = y0 + △y

采用矩阵表达上述如下：

上述也类似与图像的平移，通过上述矩阵我们发现，只需要修改矩阵右上角的 2 个元素就可以了。

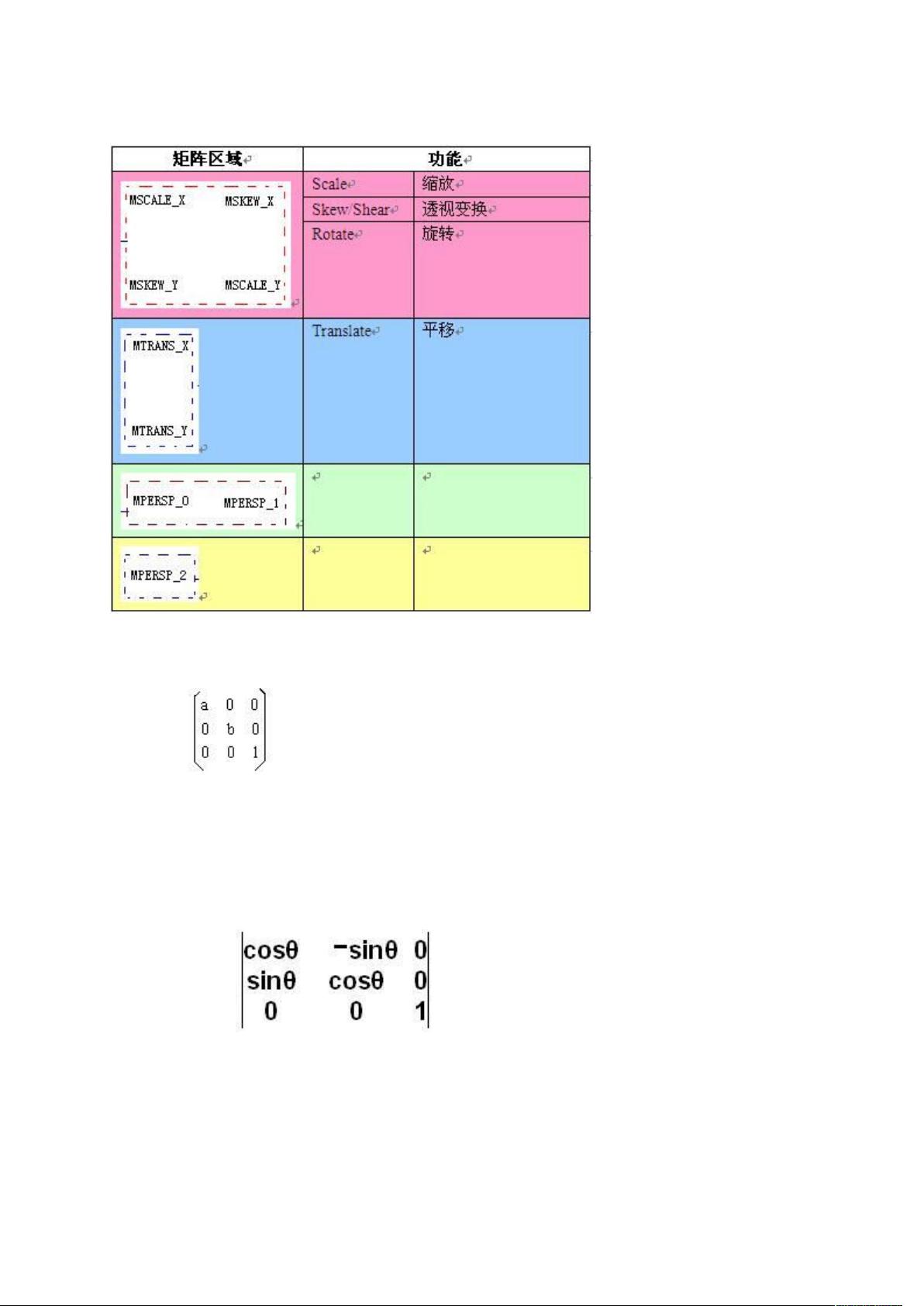
我们回头看上述矩阵的划分：

为了验证上面的功能划分，我们举个具体的例子：现设点 P0（x0 ，y0）进行平移后，移到 P（x，y），其中 x 放大 a 倍，

y 放大 b 倍，

矩阵就是：，按照类似前面“平移”的方法就验证。

图像的旋转稍微复杂：现设点 P0（x0， y0）旋转 θ 角后的对有点为 P（x， y）。通过使用向量，我们得到如下：

x0 = r cosα

y0 = r sinα

x = r cos(α-θ) = x0 cosθ+ y0 sinθ

y = r sia(α-θ) = -x0 sinθ+y0 cosθ

于是我们得到矩阵：

如果图像围绕着某个点(a ，b)旋转呢？则先要将坐标平移到该点，再进行旋转，然后将旋转后的图像平移回到原来的坐标

原点，在后面的篇幅中我们将详细介绍。

Matrix 学习——如何使用 Matrix

上一篇幅 Matrix 学习——基础知识，从高等数学方面给大家介绍了 Matrix，本篇幅我们就结合 Android 中的

android.graphics.Matrix 来具体说明，还记得我们前面说的图像旋转的矩阵：

从最简单的旋转 90 度的是：

在 android.graphics.Matrix 中有对应旋转的函数：

Matrix matrix = new Matrix();

matrix.setRotate(90);

Test.Log(MAXTRIX_TAG,”setRotate(90):%s” , matrix.toString());

查看运行后的矩阵的值（通过 Log 输出）：

剩余11页未读，继续阅读

C++实验内容：假设square_matrix是n阶整型方阵，请实现下列运算：（1）cin>> square_matrix （2）cout<< square_matrix （3）IntMatrix(n)生成一个n阶单位矩阵（4）square_matrix+IntMatrix(n) （5）square_matrix_A=square_matrix_B

下面是 C++ 实现： ```c++ #include <iostream> using namespace std; class IntMatrix { private: int **matrix; // 二维动态数组 int n; // 方阵阶数 public: // 构造函数，创建一个 n 阶方阵，默认为零矩阵 IntMatrix(int n) {

Matrix4f 资源释放

Matrix4f 是一个矩阵类，其内部所占用的资源包括内存空间和存储的数据。如果你使用的是 C++，可以通过 delete 操作符来释放内存空间，代码示例如下： ``` Matrix4f* matrix = new Matrix4f(); // 操作 matrix 对象 delete matrix; ``` 如果你使用的是 Java，可以使用 Java 的垃圾回收机制来自动释放内存空间，代码示

matrix analysis pdf

### 回答1： Matrix analysis（矩阵分析）是一门数学领域的学科，研究矩阵及其性质和应用。该学科主要包括对各种类型的矩阵进行分析，研究它们的特征值、特征向量、奇异值等性质，以及它们在线性代数、数值计算、统计学等领域的应用。 Matrix analysis在理论和实际问题中都发挥着重要作用。首先，它在线性代数中扮演着核心的角色，是研究线性方程组、线性映射和变换的重要工具。通过研究矩

写一个c代码解决下列问题：def rotate_matrix(matrix): n = len(matrix) # 逆时针旋转 90 度 for i in range(n): for j in range(i, n): matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j] # 反转每一行字符串 for i in range(n): matrix[i] = matrix[i][::-1] return matrix

好的，以下是一个用 C 语言实现的代码，可以实现字符矩阵逆时针旋转 90 度的功能： ```c #include <stdio.h> #include <stdlib.h> #include <string.h> void rotate_matrix(char **matrix, int n) { // 逆时针旋转 90 度 for (int i = 0; i < n; i++

Eigen matrix2Xf

Eigen::Matrix2Xf is a dynamic-size matrix class in the Eigen library, specifically designed for floating-point types. It represents a matrix with 2 rows and a variable number of columns, where the num

Vanvvvvvv

粉丝: 0
资源: 7

上传资源快速赚钱

我的内容管理收起

我的资源快来上传第一个资源

我的收益

登录查看自己的收益

我的积分登录查看自己的积分

我的C币登录后查看C币余额

我的收藏

我的下载

下载帮助

会员权益专享

Android Matrix理论与应用详解

评论0

会员权益专享

最新资源

Android Matrix理论与应用详解

评论0

关于android Matrix的使用

android matrix mappoint坐标系问题

android中如何获得Matrix

python中matrix函数的用法

安卓 Matrix是什麼

详解使用python绘制混淆矩阵（confusion_matrix）

scaleType="matrix"

gtsam::Matrix3d用法对不对

model.matrix()的用法

matrix computations 4th edition

random matrix theory and wireless communications pdf

android Bitmap用法总结

matrix analysis rajenda 中文影印

列举matrix.h函数库中各函数的中文意思及其用法

C++实验内容： 假设square_matrix是n阶整型方阵，请实现下列运算： （1）cin>> square_matrix （2）cout<< square_matrix （3）IntMatrix(n)生成一个n阶单位矩阵 （4）square_matrix+IntMatrix(n) （5）square_matrix_A=square_matrix_B

Matrix4f 资源释放

matrix analysis pdf

写一个c代码解决下列问题：def rotate_matrix(matrix): n = len(matrix) # 逆时针旋转 90 度 for i in range(n): for j in range(i, n): matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j] # 反转每一行字符串 for i in range(n): matrix[i] = matrix[i][::-1] return matrix

Eigen matrix2Xf

会员权益专享

最新资源

C++实验内容：假设square_matrix是n阶整型方阵，请实现下列运算：（1）cin>> square_matrix （2）cout<< square_matrix （3）IntMatrix(n)生成一个n阶单位矩阵（4）square_matrix+IntMatrix(n) （5）square_matrix_A=square_matrix_B