没有合适的资源?快使用搜索试试~ 我知道了~
首页sklearn中文指导手册0.21.3.pdf
sklearn中文指导手册0.21.3.pdf
需积分: 50 47 下载量 114 浏览量
更新于2023-05-10
评论 2
收藏 26.47MB PDF 举报
sklearn中文指导手册0.21.3是在github上下载的markdown文件整理而成,markdown文件比较散,整理成pdf方便查阅
资源详情
资源评论
资源推荐

1. 监督学习
1.1. 广义线性模型
1.1.1. 普通最小二乘法
1.1.2. 岭回归
1.1.3. Lasso
1.1.4. 多任务 Lasso
1.1.5. 弹性网络
1.1.6. 多任务弹性网络
1.1.7. 最小角回归
1.1.8. LARS Lasso
1.1.9. 正交匹配追踪法(OMP)
1.1.10. 贝叶斯回归
1.1.11. logistic 回归
1.1.12. 随机梯度下降, SGD
1.1.13. Perceptron(感知器)
1.1.14. Passive Aggressive Algorithms(被动攻击算法)
1.1.15. 稳健回归(Robustness regression): 处理离群点(outliers)和模型错误
1.1.16. 多项式回归:用基函数展开线性模型
1.2. 线性和二次判别分析
1.2.1. 使用线性判别分析来降维
1.2.2. LDA 和 QDA 分类器的数学公式
1.2.3. LDA 的降维数学公式
1.2.4. Shrinkage(收缩)
1.2.5. 预估算法
1.3. 内核岭回归
1.4. 支持向量机
1.4.1. 分类
1.4.2. 回归
1.4.3. 密度估计, 异常(novelty)检测
1.4.4. 复杂度
1.4.5. 使用诀窍
1.4.6. 核函数
1.4.7. 数学公式
1.4.8. 实现细节
1.5. 随机梯度下降
1.5.1. 分类
1.5.2. 回归
1.5.3. 稀疏数据的随机梯度下降
1.5.4. 复杂度
1.5.5. 停止判据
1.5.6. 实用小贴士
1.5.7. 数学描述
1.5.8. 实现细节
1.6. 最近邻
1.6.1. 无监督最近邻
1.6.2. 最近邻分类

1.6.3. 最近邻回归
1.6.4. 最近邻算法
1.6.5. 最近质心分类
1.6.6. 邻域成分分析
1.7. 高斯过程
1.7.1. 高斯过程回归(GPR)
1.7.2. GPR 示例
1.7.3. 高斯过程分类(GPC)
1.7.4. GPC 示例
1.7.5. 高斯过程内核
1.8. 交叉分解
1.9. 朴素贝叶斯
1.9.1. 高斯朴素贝叶斯
1.9.2. 多项分布朴素贝叶斯
1.9.3. 补充朴素贝叶斯
1.9.4. 伯努利朴素贝叶斯
1.9.5. 基于外存的朴素贝叶斯模型拟合
1.10. 决策树
1.10.1. 分类
1.10.2. 回归
1.10.3. 多值输出问题
1.10.4. 复杂度分析
1.10.5. 实际使用技巧
1.10.6. 决策树算法: ID3, C4.5, C5.0 和 CART
1.10.7. 数学表达
1.11. 集成方法
1.11.1. Bagging meta-estimator(Bagging 元估计器)
1.11.2. 由随机树组成的森林
1.11.3. AdaBoost
1.11.4. Gradient Tree Boosting(梯度树提升)
1.11.5. Voting Classifier(投票分类器)
1.11.6. 投票回归器(Voting Regressor)
1.12. 多类和多标签算法
1.12.1. 多标签分类格式
1.12.2. 1对其余
1.12.3. 1对1
1.12.4. 误差校正输出代码
1.12.5. 多输出回归
1.12.6. 多输出分类
1.12.7. 链式分类器
1.13. 特征选择
1.13.1. 移除低方差特征
1.13.2. 单变量特征选择
1.13.3. 递归式特征消除
1.13.4. 使用 SelectFromModel 选取特征
1.13.5. 特征选取作为 pipeline(管道)的一部分
1.14. 半监督学习
1.14.1. 标签传播
1.15. 等式回归

1.16. 概率校准
1.17. 神经网络模型(有监督)
1.17.1. 多层感知器
1.17.2. 分类
1.17.3. 回归
1.17.4. 正则化
1.17.5. 算法
1.17.6. 复杂度
1.17.7. 数学公式
1.17.8. 实用技巧
1.17.9. 使用 warm_start 的更多控制
{% raw %}
1.1. 广义线性模型
校验者:
@专业吹牛逼的小明
@Gladiator
@Loopy
@qinhanmin2014
翻译者:
@瓜牛
@年纪大了反应慢了
@Hazekiah
@BWM-蜜蜂
本章主要讲述一些用于回归的方法,其中目标值 y 是输入变量 x 的线性组合。 数学概念表示为:如果
是预测值,那么有:
在整个模块中,我们定义向量 作为 coef_ ,定义 作为 intercept_ 。
如果需要使用广义线性模型进行分类,请参阅 logistic 回归 。
1.1.1. 普通最小二乘法
LinearRegression 拟合一个带有系数 的线性模型,使得数据集实际观测数据和
预测数据(估计值)之间的残差平方和最小。其数学表达式为:

LinearRegression 会调用 fit 方法来拟合数组 X, y,并且将线性模型的系数 存储在其成员变量
coef_ 中:
然而,对于普通最小二乘的系数估计问题,其依赖于模型各项的相互独立性。当各项是相关的,且设计
矩阵 的各列近似线性相关,那么,设计矩阵会趋向于奇异矩阵,这种特性导致最小二乘估计对于随
机误差非常敏感,可能产生很大的方差。例如,在没有实验设计的情况下收集到的数据,这种多重共线
性(multicollinearity)的情况可能真的会出现。
示例:
线性回归示例
1.1.1.1. 普通最小二乘法的复杂度
{% endraw %}
该方法使用 X 的奇异值分解来计算最小二乘解。如果 X 是一个形状为 (n_samples, n_features) 的
矩阵,设 $$ n{samples} \geq n{features} $$ , 则该方法的复杂度为 $$ O(n{samples} n{fearures}^2)
$$
{% raw %}
1.1.2. 岭回归
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5, 0.5])
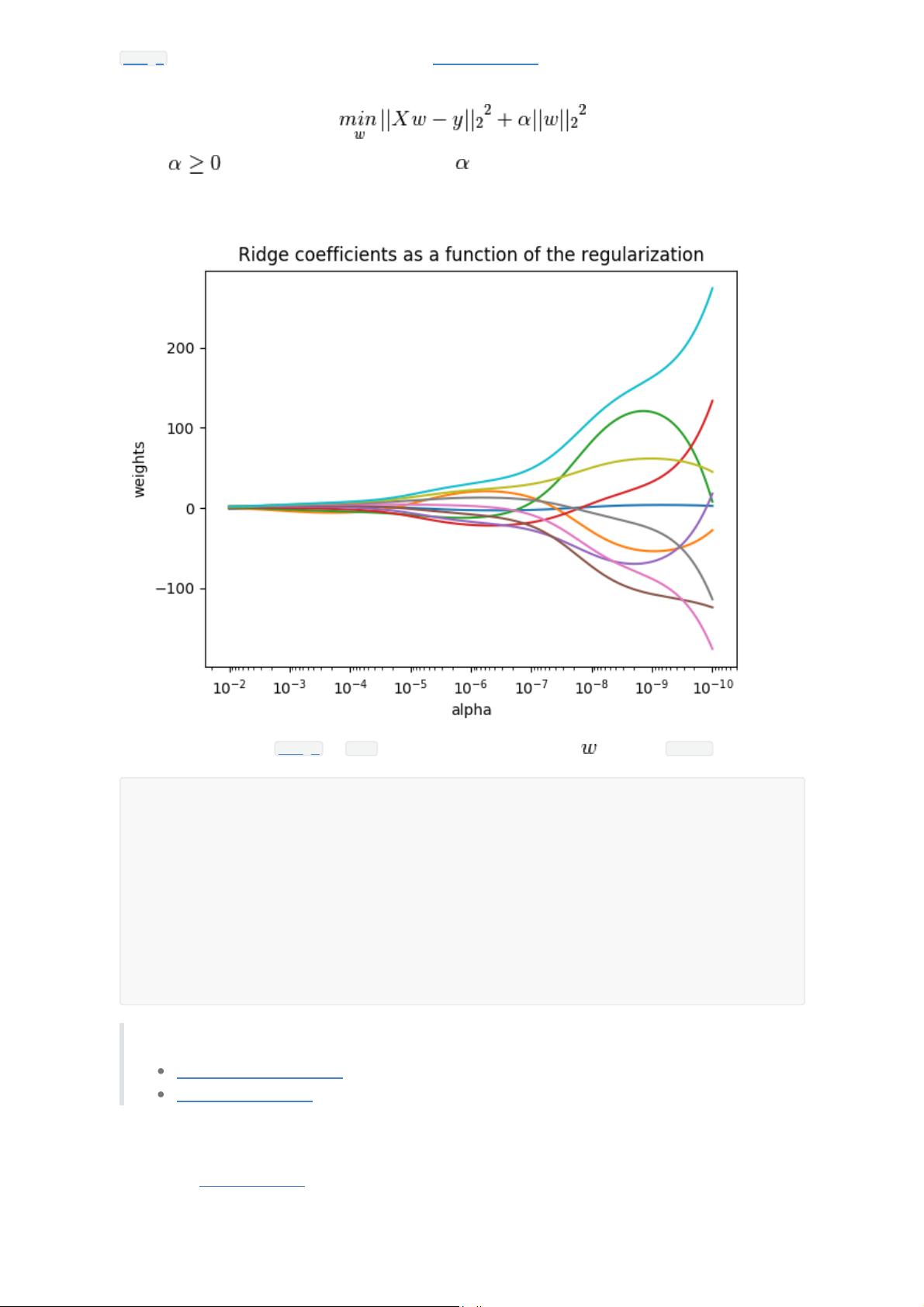
Ridge 回归通过对系数的大小施加惩罚来解决 普通最小二乘法 的一些问题。 岭系数最小化的是带罚项
的残差平方和,
其中, 是控制系数收缩量的复杂性参数: 的值越大,收缩量越大,模型对共线性的鲁棒性
也更强。
与其他线性模型一样, Ridge 用 fit 方法完成拟合,并将模型系数 存储在其 coef_ 成员中:
示例:
岭系数对回归系数的影响
分类特征稀疏的文本
1.1.2.1. 岭回归的复杂度
这种方法与 普通最小二乘法 的复杂度是相同的.
1.1.2.2. 设置正则化参数:广义交叉验证
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...
剩余425页未读,继续阅读
萌休瘫
- 粉丝: 1
- 资源: 6
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- RTL8188FU-Linux-v5.7.4.2-36687.20200602.tar(20765).gz
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0