自动控制原理复习精要：传递函数与结构图简化

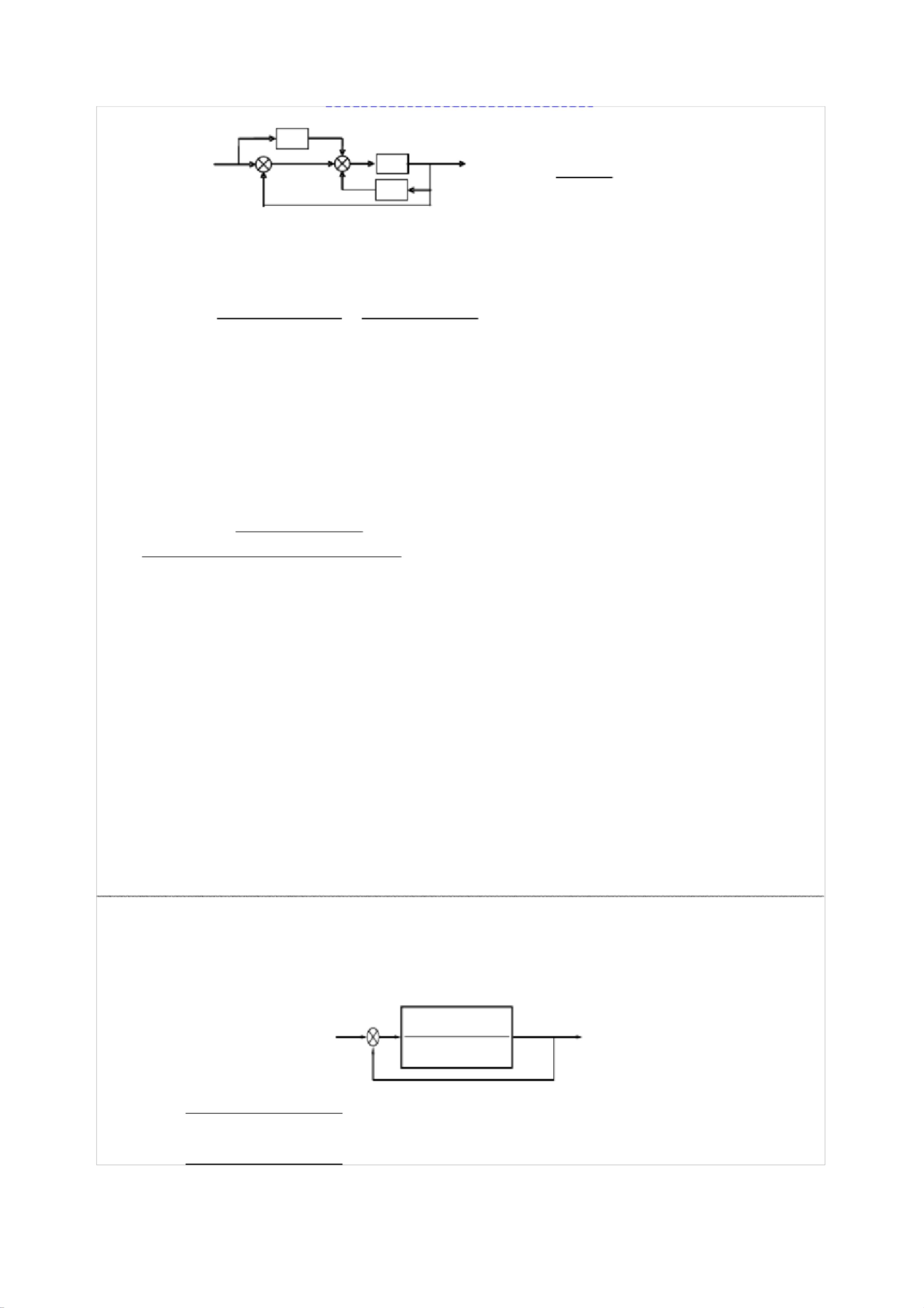
"超详细自动控制原理复习总结(精华版).pdf" 自动控制原理是电气工程、自动化、航空航天等多个领域中的核心课程，它涉及到系统稳定、性能分析和控制器设计等内容。本复习总结主要聚焦于自动控制系统的数学建模、等效变换和简化方法。 一、系统数学模型 自动控制系统有三种基本的数学模型：时域模型（微分方程）、复域模型（传递函数）和频域模型（频率特性）。传递函数是重点，它定义为在零初始条件下，系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。理解这一概念对于分析系统动态响应至关重要。 二、结构图的等效变换与简化 结构图等效变换的目标是消除中间变量，得到系统的总传递函数。等效变换应保持系统在输入与输出之间的关系不变。基本的连接方式包括串联、并联和反馈连接。处理复杂结构图时，可以运用移出引出点或比较点的方法。具体规则如下： - 引出点前移：移动支路上乘以引出点处的传递函数。 - 引出点后移：移动支路上乘以1/引出点处的传递函数。 - 相加点前移：移动支路上乘以1/相加点处的传递函数。 - 相加点后移：移动支路上乘以相加点处的传递函数。 例如，在求解系统的传递函数C(s)/R(s)时，可以先通过等效变换和反馈消除法逐步简化结构图，最终得到系统的传递函数表达式。 三、应用实例 解法通常包括以下步骤： 1. 明确结构图中的串联、并联和反馈连接关系。 2. 移动引出点或相加点，按照上述规则进行等效变换。 3. 消除反馈连接，通常使用反馈因子表示反馈部分。 4. 逐步简化结构，直到得到系统总传递函数。 四、总结 自动控制原理的学习不仅要求理解基本概念，还需要掌握数学模型的转换和简化技巧。这有助于对系统的动态性能进行深入分析，从而设计出满足特定性能指标的控制器。在实际工程应用中，这些知识是实现自动化设备和系统稳定、高效运行的基础。