傅里叶变换与系统频域分析详解

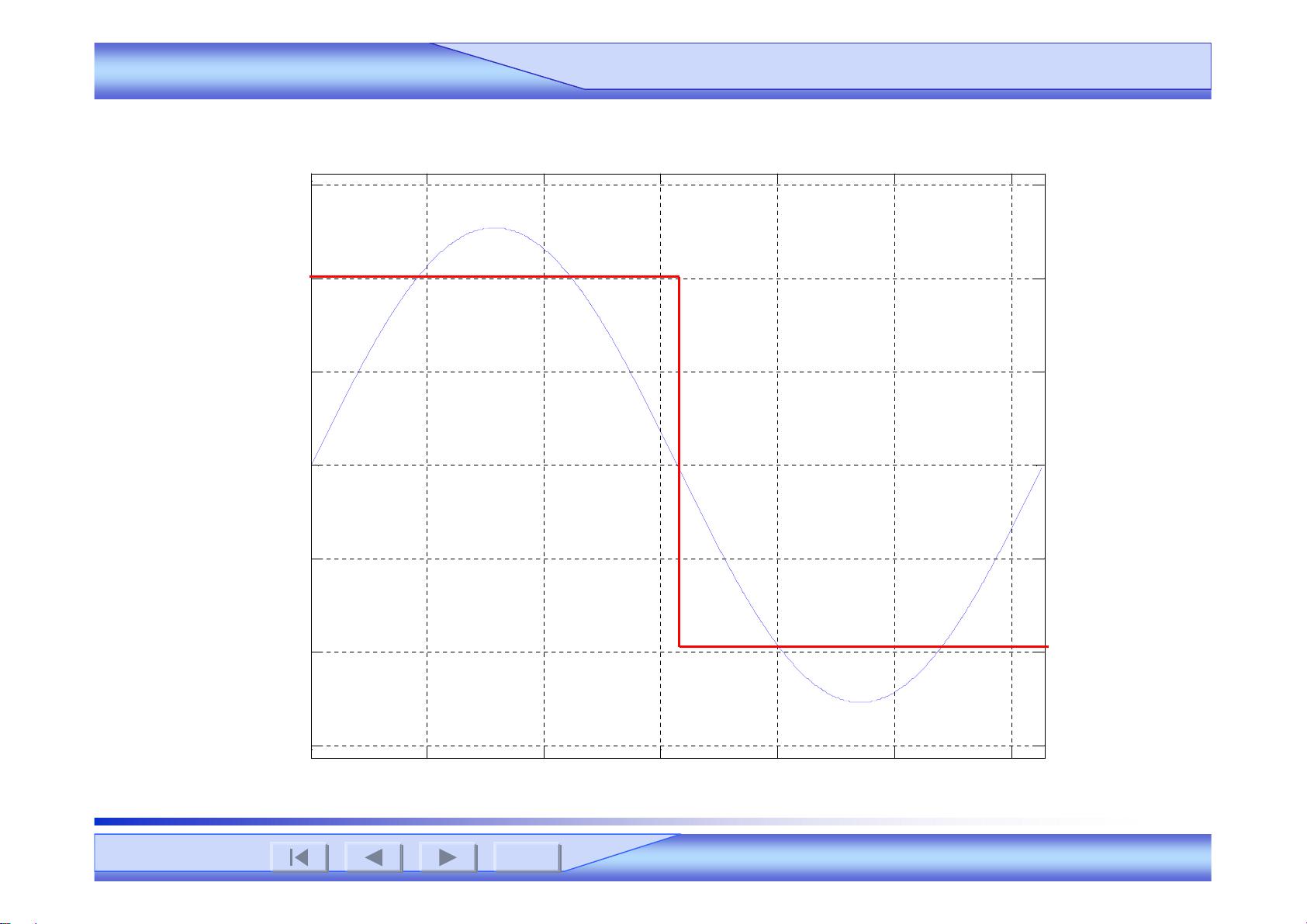
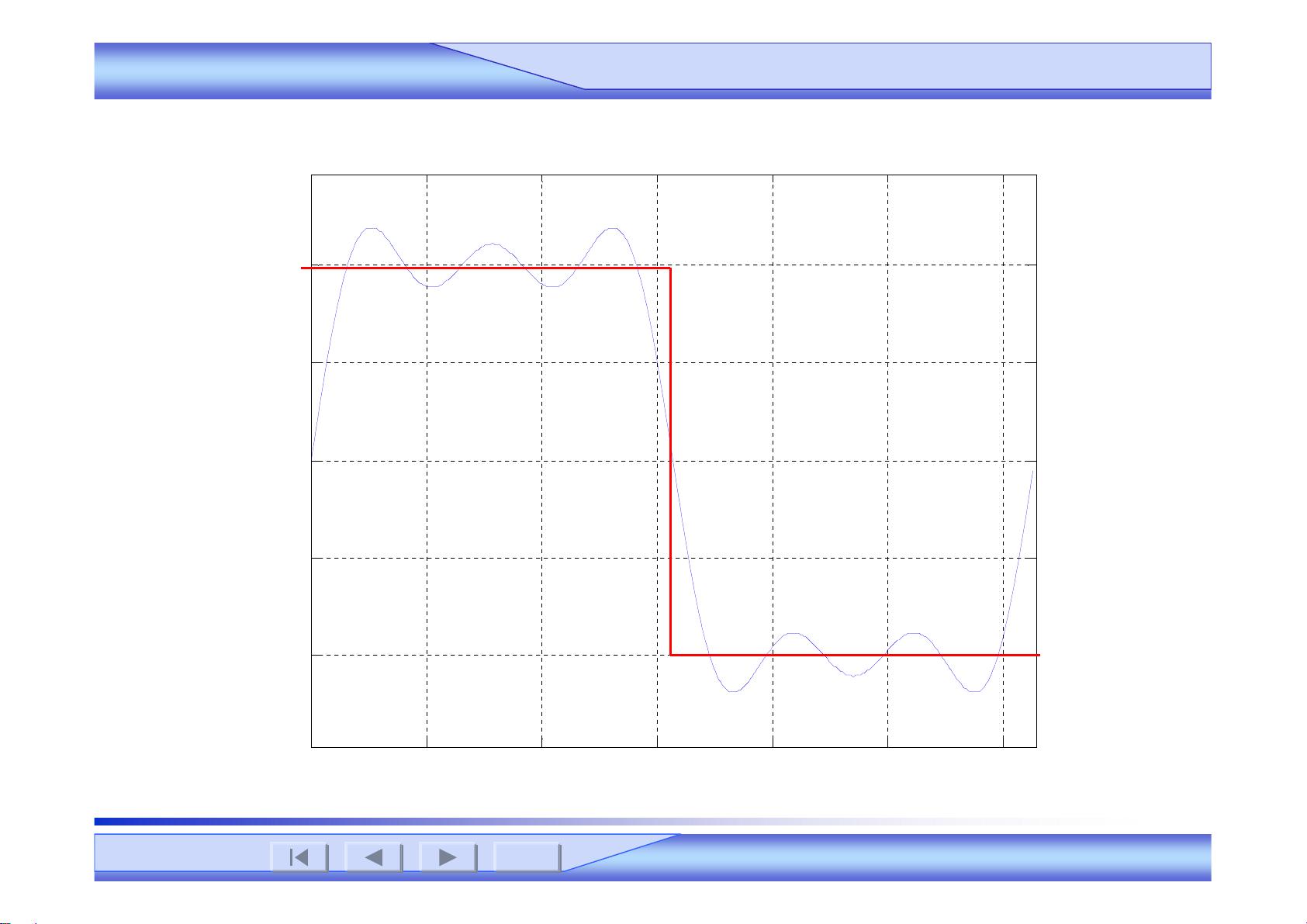
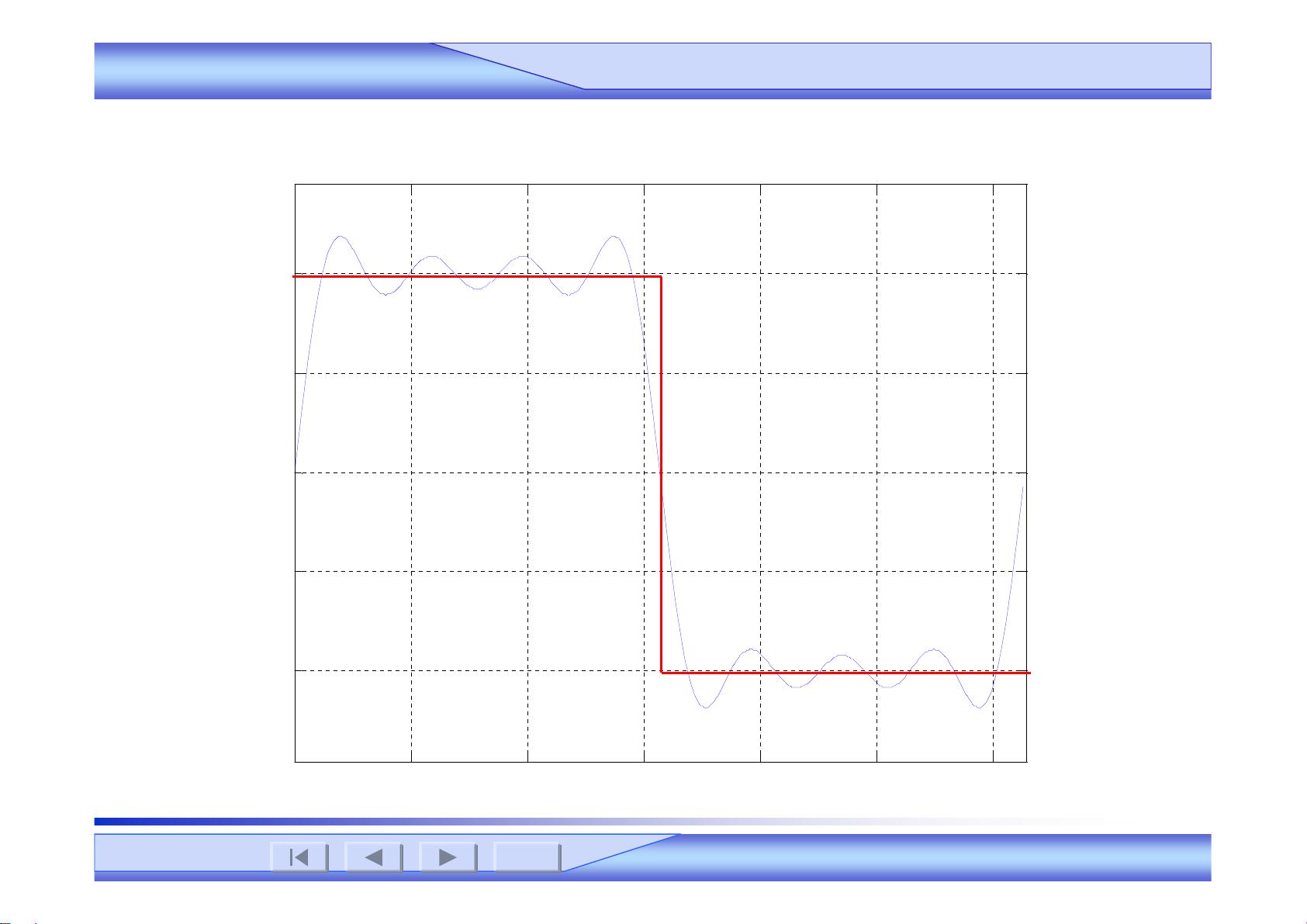
"傅里叶变换和系统的频域分析" 傅里叶变换是信号处理和系统分析中的核心概念，它将时域中的信号转化为频域表示，揭示了信号的频率成分。这一转换对于理解和设计电子系统，特别是通信、图像处理和控制理论等领域具有重要意义。 在第4章"傅里叶变换和系统的频域分析"中，首先介绍了正交函数集的概念，这是傅里叶变换的基础，允许我们将复杂信号分解为简单的正交函数，如正弦和余弦波。接着，详细讨论了周期信号的傅里叶级数，包括如何将周期信号分解为正弦和余弦项，以及如何处理奇函数和偶函数的傅里叶级数。傅里叶级数的指数形式则提供了一种更简洁的表示方法。 周期信号的频谱是傅里叶变换的直接应用，它展示了信号在频率域内的分布。以周期矩形脉冲为例，解释了如何计算其频谱，并引出了周期信号的功率概念。非周期信号的频谱通过傅里叶变换来描述，扩展了分析非周期性信号的可能性，同时也涵盖了奇异函数的傅里叶变换。 傅里叶变换的性质是理解和应用变换的关键，包括线性性质、奇偶性、对称性、尺度变换、时移和频移特性、卷积定理、时域微分和积分、频域微分和积分以及相关定理。这些性质提供了分析系统和处理信号的工具。 在系统的频域分析中，频率响应是理解线性时不变（LTI）系统行为的重要指标，无失真传输是设计系统时追求的理想状态，而理想低通滤波器的响应则是滤波理论的基本模型。取样定理则解释了如何在不失真的情况下从连续信号中取样，并在时域和频域中理解这一过程。 对于离散信号的处理，介绍了周期序列的离散傅里叶级数（DFS）和非周期序列的离散时间傅里叶变换（DTFT），这是数字信号处理的基础。离散傅里叶变换（DFT）及其性质是数字信号处理的核心，广泛应用于计算机科学和工程中。 最后，傅里叶变换的历史源于19世纪初法国数学家傅里叶的工作，他在热传导问题的研究中提出了将任意函数表示为三角函数级数的方法，奠定了现代傅里叶分析的基础。 傅里叶变换和系统的频域分析是理解和解决实际工程问题的关键，它们为信号处理、通信网络和控制系统的设计提供了强大的理论支持。