线性阀体设计：内筒优化与最小二乘法

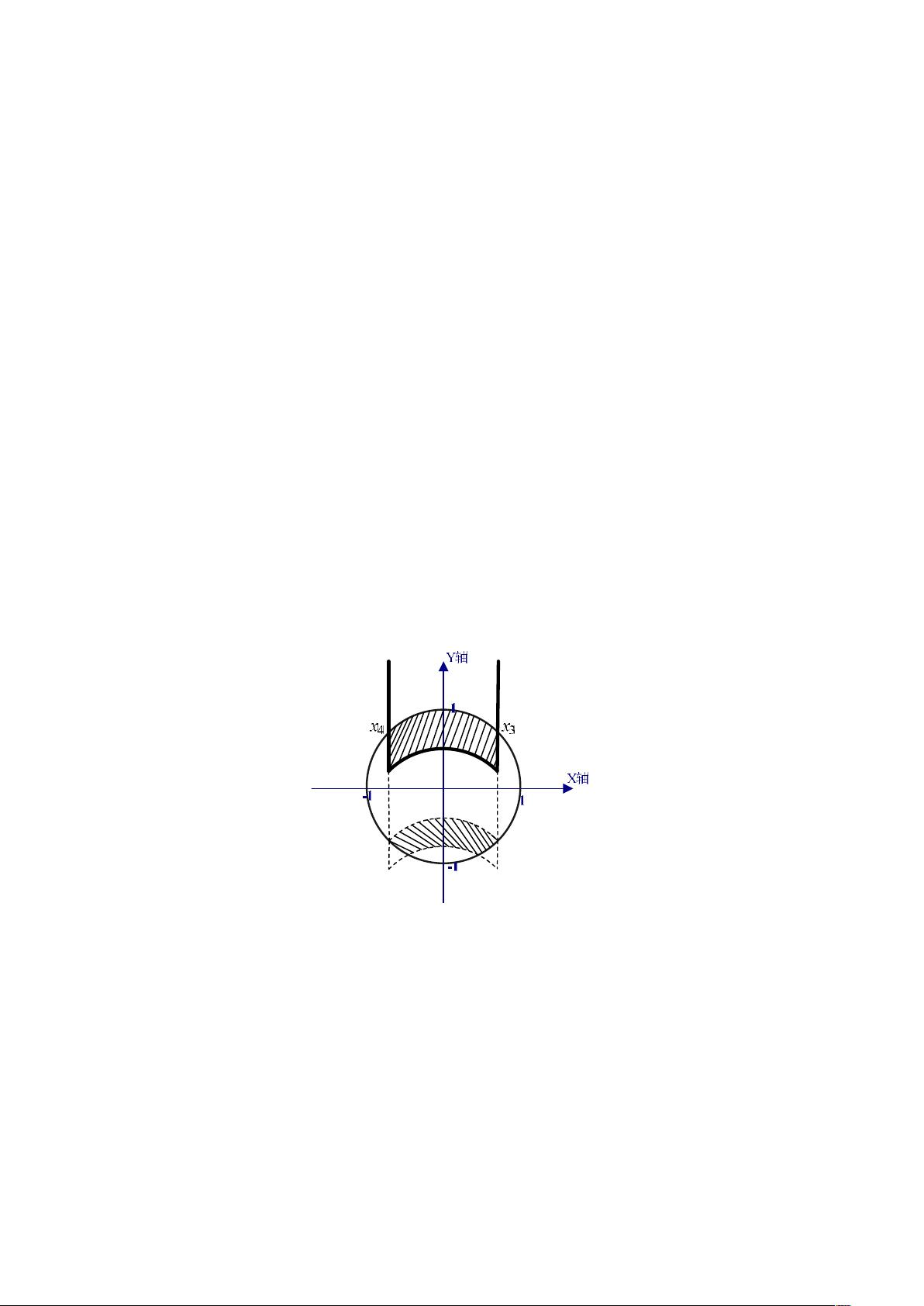
"这篇文档是关于第三届研究生数学建模竞赛中的C题，即维修线性流量阀时的内筒设计问题。文章探讨了如何通过优化内筒设计来实现阀体旋转角度与流量的线性关系，主要涉及了线性阀体设计、数学模型构建、最优化方法以及应对磨损的策略。" 在实际应用中，线性流量阀体的需求日益增加，因为这种阀门能够确保旋转角度与流量之间的精确线性关系，从而便于流量的精确控制。文档指出，传统的阀体设计往往无法达到理想的线性特性。作者对此进行了深入研究，旨在找到一种能保持线性流量特性的内筒设计。 首先，研究者通过分析四种特定形状的内孔，发现凸凹圆曲线能够使"过流面积"随曲线下降距离的变化保持较好的线性关系。他们运用微元法证明了当过流面积严格线性变化时，曲线与外孔交点的横坐标差为常数，这意味着在交点处曲线的斜率应趋向无穷大，以维持线性特性。 为了解决这个问题，文档应用了最小二乘原理，建立了一个无约束的泛函极值模型，并利用变分法将其转换为微分方程。通过Ritz算法，研究人员找到了一个接近理想线性关系的内孔曲线形状。这个设计方案的样本点偏差平方和较小，仅为0.064412，显示出良好的线性表现。 对于更复杂的情况，即需要同时满足两个约束条件（流量下限和上限），文档提出了有约束的泛函极值模型。通过调整内孔形状，尽管会牺牲一定的线性关系，但可以确保阀体在限制条件下工作。最终，找到了一个适应这两个约束的内孔设计方案。 此外，针对外孔可能出现的磨损问题，文章提出了一种结合自动控制理论和逆向工程技术的解决方案，以确保即使在外孔磨损后，内筒设计仍能保持其功能。 这篇文档详细阐述了线性流量阀体内筒设计的数学模型和优化方法，展示了从特殊形状内孔中获取启发并应用于实际问题的建模过程。关键词包括线性阀体、最小二乘法、泛函极值模型、变分原理和非线性规划，这表明研究涵盖了多个数学和工程领域的交叉点。该研究对于理解和改进线性阀体设计具有重要的理论和实践意义。