梯度下降算法深度解析与代码实现

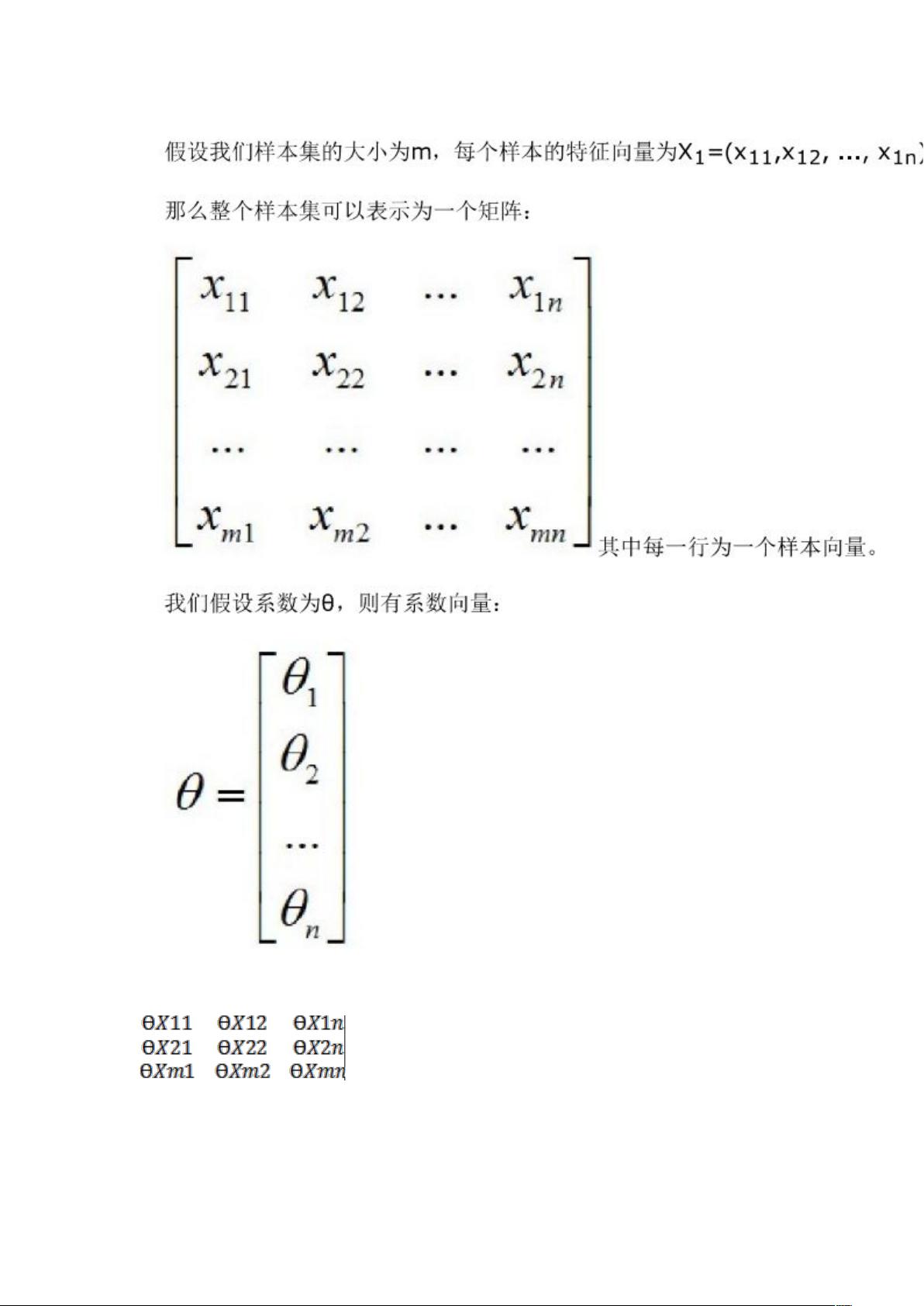
"梯度下降是一种优化算法，广泛应用于机器学习和深度学习中，用于找到损失函数最小化的参数。本文将深入探讨梯度下降的原理和应用，通过实例和简单的代码示例帮助读者理解其工作方式。" 梯度下降算法在机器学习中扮演着至关重要的角色，它是一种迭代优化方法，主要用于找到函数的局部最小值。在这个场景中，函数通常是损失函数，而我们试图最小化这个函数以获得最佳模型参数。例如，在房价预测问题中，我们希望找到一个公式，如f(x) = w1*x1 + w2*x2 + ... + wn*xn，其中w1, w2, ..., wn是待确定的权重，x1, x2, ..., xn是房子的特征（如面积、方位等），目标是预测房价y。 梯度下降的核心思想是沿着损失函数梯度的反方向移动，因为梯度的方向指向函数增长最快的方向，所以反方向则是下降最快的方向。在每一步迭代中，参数都会更新，使得损失函数的值逐渐减小，直到达到局部最小值或满足停止条件。 1. 损失函数（Loss Function）：损失函数是用来衡量模型预测结果与实际值之间的差距。对于线性回归问题，通常使用均方误差（Mean Squared Error, MSE）作为损失函数，即J(w) = (1/2n) * Σ((h(x_i) - y_i)^2)，其中n是样本数量，h(x_i)是模型预测值，y_i是真实值。 2. 梯度计算：在梯度下降中，我们需要计算损失函数关于每个参数的偏导数，这些偏导数组成的向量被称为梯度。对于线性回归，梯度是J(w)对w的偏导数，即∇J(w) = (1/n) * Σ((h(x_i) - y_i) * x_i)。 3. 参数更新：在每一轮迭代中，参数w会根据梯度和学习率α进行更新，w := w - α * ∇J(w)。学习率决定了每次迭代时参数更新的步长，过大会导致不稳定性，过小则收敛速度慢。 4. 迭代过程：重复计算梯度并更新参数，直到梯度接近于零（达到局部最小值）或者达到预设的迭代次数。 在实际应用中，还存在批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-Batch Gradient Descent）等变体，它们主要区别在于每次迭代中使用多少样本计算梯度，这会影响算法的收敛速度和精度。 简单的Python代码示例： ```python import numpy as np def gradient_descent(X, y, w, learning_rate, num_iterations): n_samples, n_features = X.shape for _ in range(num_iterations): gradients = (1 / n_samples) * np.dot(X.T, (np.dot(X, w) - y)) w -= learning_rate * gradients return w # 假设X是特征矩阵，y是目标值，初始权重w为零 X = np.array([[4, 3], [5, 2], [6, 1]]) y = np.array([100, 95, 105]) w = np.zeros(2) learning_rate = 0.01 num_iterations = 1000 optimal_w = gradient_descent(X, y, w, learning_rate, num_iterations) print("Optimal weights:", optimal_w) ``` 以上代码实现了一个简单的批量梯度下降算法，对给定的特征矩阵X和目标值y进行训练，求得最佳的权重w。请注意，这只是一个基础示例，实际应用中还需要考虑正则化、初始化策略、早停等优化措施。