【基础】梯度下降算法原理详解及MATLAB程序代码

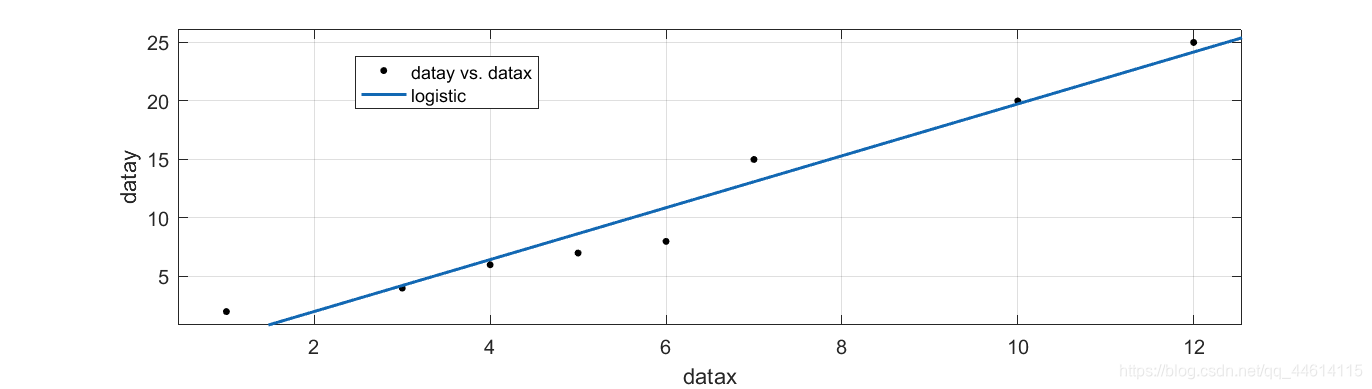
# 1. 梯度下降算法概述**

梯度下降算法是一种迭代优化算法，用于寻找函数的局部最小值。它通过沿函数梯度的负方向迭代更新参数，从而逐步逼近最优解。梯度下降算法在机器学习和深度学习领域有着广泛的应用，因为它能够有效地优化复杂的非线性函数。

# 2. 梯度下降算法原理

### 2.1 梯度概念和梯度计算

**梯度概念**

梯度是一个向量，它表示函数在某一点处的变化率。对于一个多变量函数 `f(x1, x2, ..., xn)`，其在点 `(x1, x2, ..., xn)` 处的梯度为：

∇f(x1, x2, ..., xn) = [∂f/∂x1, ∂f/∂x2, ..., ∂f/∂xn]

其中，`∂f/∂xi` 表示函数 `f` 对变量 `xi` 的偏导数。

**梯度计算**

梯度可以通过以下方法计算：

- **解析方法：**直接计算函数的偏导数。
- **数值方法：**使用有限差分或其他数值方法近似计算偏导数。

### 2.2 梯度下降算法的数学原理

梯度下降算法是一种迭代算法，用于寻找函数的局部最小值。算法从一个初始点开始，然后沿着函数梯度的负方向迭代更新点的位置，直到达到局部最小值。

**数学原理**

梯度下降算法的数学原理如下：

x_new = x_old - α * ∇f(x_old)

其中：

- `x_old` 是当前点
- `x_new` 是更新后的点
- `α` 是学习率，控制步长大小
- `∇f(x_old)` 是当前点的梯度

**学习率**

学习率 `α` 是梯度下降算法中的一个重要参数。它控制步长大小，影响算法的收敛速度和准确性。学习率过大会导致算法不稳定，过小会导致算法收敛速度慢。

### 2.3 梯度下降算法的变种

标准梯度下降算法存在一些缺点，例如收敛速度慢和容易陷入局部最小值。为了解决这些问题，提出了多种梯度下降算法的变种：

**动量梯度下降算法**

动量梯度下降算法通过引入动量项来加速收敛速度。动量项记录了梯度的历史变化，并将其添加到当前梯度中，从而使算法在收敛方向上具有更大的步长。

**RMSprop 算法**

RMSprop 算法通过自适应调整学习率来提高收敛速度和稳定性。它计算梯度的均方根（RMS），并将其用于调整学习率。

**Adam 算法**

Adam 算法结合了动量和 RMSprop 算法的优点，是一种高效且鲁棒的梯度下降算法变种。它使用动量和自适应学习率，在各种机器学习任务中表现出色。

# 3. 梯度下降算法MATLAB实现

### 3.1 MATLAB中梯度下降算法的函数实现

MATLAB提供了多种函数来实现梯度下降算法，其中最常用的是`fminunc`函数。`fminunc`函数是一个无约束优化函数，它使用拟牛顿方法来最小化一个标量函数。

`fminunc`函数的语法如下：

x = fminunc(fun, x0, options)

其中：

* `fun`是需要最小化的标量函数的句柄。
* `x0`是优化变量的初始值。
* `op