【实战演练】MATLAB在天气模式分析中的应用：使用偏微分方程模拟气候变化

# 1. MATLAB在天气模式分析中的理论基础**

MATLAB是一种强大的技术计算语言，在天气模式分析中发挥着至关重要的作用。它提供了广泛的工具和算法，用于解决天气预测和气候变化模拟中遇到的复杂计算问题。

MATLAB在天气模式分析中的应用主要基于偏微分方程（PDE）的求解。PDE是一类数学方程，用于描述物理系统中连续变化的现象，如天气模式。MATLAB提供了强大的工具，可以有效地求解PDE，从而模拟天气模式的演变。

# 2. 偏微分方程在气候变化模拟中的应用

偏微分方程 (PDE) 在气候变化模拟中扮演着至关重要的角色，因为它可以描述大气和海洋环流等复杂系统的时空演变。本节将探讨 PDE 在气候变化模拟中的应用，包括 PDE 的类型、求解方法以及在气候变化模型中的具体应用。

### 2.1 偏微分方程的类型和求解方法

#### 2.1.1 常用偏微分方程的分类

PDE 根据其阶数和未知函数的个数进行分类。常用的 PDE 类型包括：

- **一级偏微分方程：**未知函数只对一个自变量求导，如一维波动方程。
- **二阶偏微分方程：**未知函数对两个自变量求导，如拉普拉斯方程和泊松方程。
- **抛物型偏微分方程：**未知函数对时间求导，且空间导数为二阶，如热方程。
- **双曲型偏微分方程：**未知函数对时间求导，且空间导数为二阶，但与抛物型 PDE 不同的是，双曲型 PDE 的特征线是实数直线，如波动方程。
- **椭圆型偏微分方程：**未知函数对空间导数为二阶，如拉普拉斯方程和泊松方程。

#### 2.1.2 数值解法和有限差分法

由于 PDE 通常无法解析求解，因此需要使用数值方法来近似求解。常用的数值方法包括：

- **有限差分法 (FDM)：**将 PDE 离散化成代数方程组，然后使用迭代方法求解方程组。
- **有限元法 (FEM)：**将求解域划分为有限个单元，并在每个单元内使用插值函数近似未知函数。
- **有限体积法 (FVM)：**将求解域划分为有限个体积，并应用守恒定律来求解 PDE。

FDM 是一种简单且高效的数值方法，特别适用于规则网格。其基本思想是将 PDE 中的导数用有限差分近似，然后得到一个线性方程组。通过求解方程组，可以得到未知函数在网格点上的近似值。

### 2.2 气候变化模拟中的偏微分方程模型

在气候变化模拟中，PDE 用于建立描述大气和海洋环流的数学模型。这些模型可以预测未来气候变化的趋势，并评估人类活动对气候系统的影响。

#### 2.2.1 大气环流模型

大气环流模型 (ACM) 使用 PDE 来描述大气中风的运动、温度和湿度等要素。这些模型可以预测天气模式、气候变化和极端天气事件。

一个典型的大气环流模型包括以下 PDE：

- **动量方程：**描述风的运动，考虑压力梯度力、科里奥利力、摩擦力和重力。
- **热力学方程：**描述温度和湿度的变化，考虑热量输送、辐射和相变。
- **连续性方程：**描述空气的守恒，考虑空气流入和流出。

#### 2.2.2 海洋环流模型

海洋环流模型 (OCM) 使用 PDE 来描述海洋中水的运动、温度和盐度等要素。这些模型可以预测洋流、海温变化和海平面上升。

一个典型的海洋环流模型包括以下 PDE：

- **动量方程：**描述水的运动，考虑压力梯度力、科里奥利力、摩擦力和重力。
- **热力学方程：**描述温度和盐度的变化，考虑热量输送、辐射和相变。
- **连续性方程：**描述水的守恒，考虑水流入和流出。

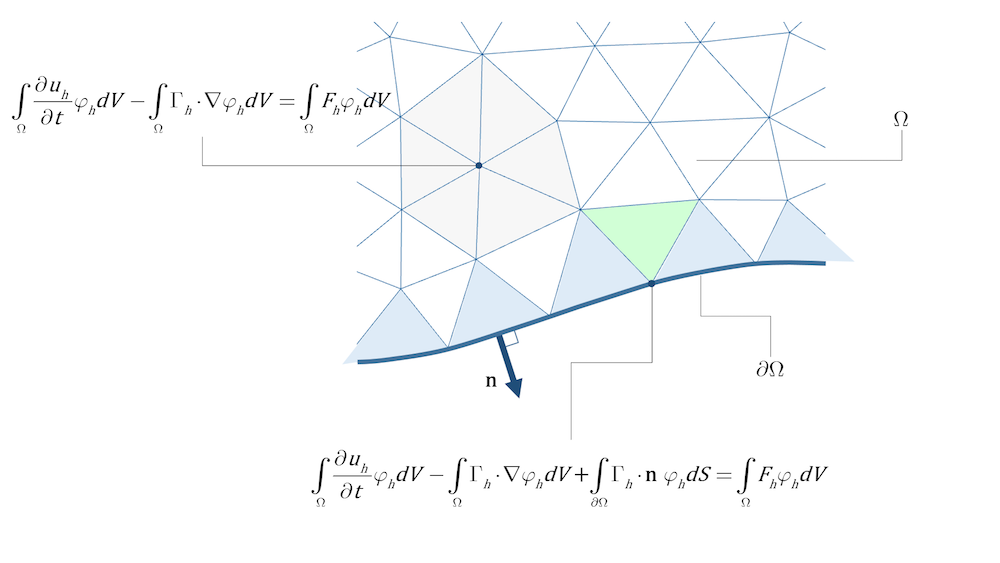
# 3.1 MATLAB中偏微分方程求解工具箱

MATLAB中提供了pdetool工具箱，用于求解偏微分方程。该工具箱提供了交互式图形用户界面（GUI），允许用户定义偏微分方程模型、设置边界条件和初始条件，并求解方程。

#### 3.1.1 pdetool工具箱简介

pdetool工具箱包含以下主要功能：

- 定义偏微分方程模型：用户可以指定方程类型（如椭圆方程、抛物方程或双曲方程）、方程系数和边界条件。
- 设置网格：工具箱允许用户定义计算网格，包括网格类型（如三角形或四边形）、网格大小和网格边界。
- 求解方程：pdetool使用有限元法或有限差分法求解偏微分方程。
- 可视化结果：工具箱提供各种可视化工具，用于显示方程解、边界条件和网格。

#### 3.1.2 偏微分方程求解步骤

使用pdetool工具箱求解偏微分方程的一般步骤如下：

1. **定义模