【基础】MATLAB中的奇异值分解（SVD）及应用

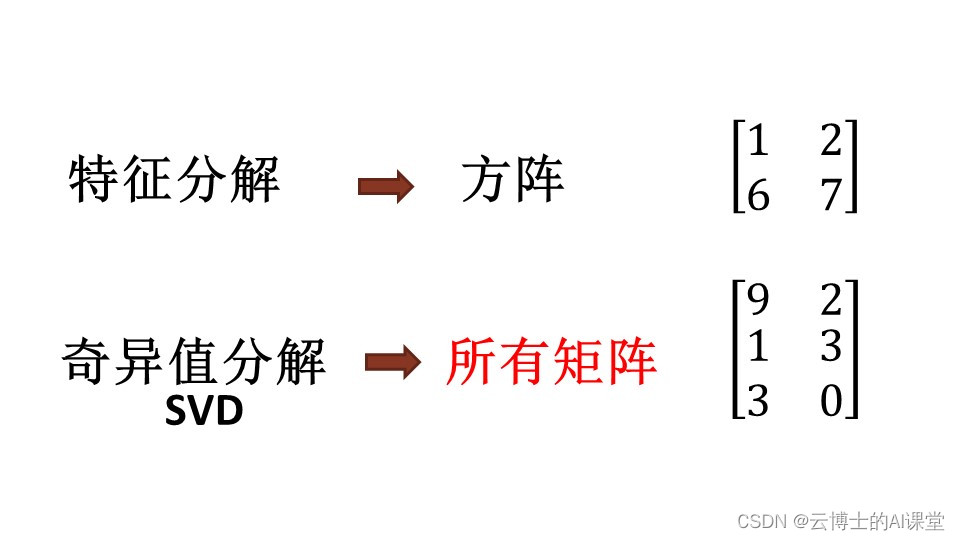
# 1. 奇异值分解（SVD）的理论基础**

奇异值分解（SVD）是一种强大的线性代数技术，用于将矩阵分解为三个矩阵的乘积：一个正交矩阵 U、一个对角矩阵 Σ 和另一个正交矩阵 V。

import numpy as np

# 矩阵 A
A = np.array([[1, 2], [3, 4]])

# 奇异值分解
U, Sigma, Vh = np.linalg.svd(A, full_matrices=False)

在 SVD 中，Σ 对角矩阵包含矩阵 A 的奇异值，即 A 的特征值的平方根。U 和 V 是正交矩阵，包含 A 的左奇异向量和右奇异向量。

# 2. SVD在图像处理中的应用

### 2.1 图像降噪

#### 2.1.1 SVD原理在图像降噪中的应用

奇异值分解（SVD）是一种强大的数学工具，广泛应用于图像处理领域，其中一个重要的应用就是图像降噪。图像降噪的目的是去除图像中的噪声，提高图像质量。SVD可以有效地将图像分解为一组奇异值和奇异向量，从而分离出图像中的噪声成分。

具体来说，SVD将图像矩阵分解为三个矩阵的乘积：

A = U * Σ * V^T

其中：

- `A` 是原始图像矩阵
- `U` 是左奇异向量矩阵
- `Σ` 是奇异值矩阵，对角线上包含图像的奇异值
- `V^T` 是右奇异向量矩阵的转置

图像中的噪声通常集中在奇异值较小的奇异向量中。因此，通过截断奇异值，可以有效地去除噪声。

#### 2.1.2 降噪算法的实现

基于SVD的图像降噪算法可以如下实现：

import numpy as np
from scipy.linalg import svd

# 读取图像
image = cv2.imread('noisy_image.jpg')

# 将图像转换为灰度图
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 进行SVD分解
U, Sigma, Vh = svd(gray_image, full_matrices=False)

# 截断奇异值
k = 100  # 截断奇异值的数量
Sigma_trunc = Sigma[:k, :k]

# 重构图像
denoised_image = np.dot(U, np.dot(Sigma_trunc, Vh))

# 显示降噪后的图像
cv2.imshow('Denoised Image', denoised_image)
cv2.waitKey(0)

**参数说明：**

- `k`：截断奇异值的数量，值越大，降噪效果越好，但图像细节损失也越大。

**代码逻辑分析：**

1. 读取图像并转换为灰度图。
2. 对灰度图进行SVD分解，得到奇异值矩阵 `Sigma`。
3. 截断奇异值，保留前 `k` 个奇异值。
4. 使用截断后的奇异值重构图像。
5. 显示降噪后的图像。

### 2.2 图像压缩

#### 2.2.1 SVD原理在图像压缩中的应用

SVD还可以用于图像压缩。图像压缩的目的是在保持图像质量的同时减小图像文件的大小。SVD可以将图像分解为一组奇异值和奇异向量，其中奇异值代表图像中最重要的信息。通过截断奇异值，可以有效地减少图像文件的大小。

#### 2.2.2 压缩算法的实现

基于SVD的图像压缩算法可以如下实现：

import numpy as np
from scipy.linalg import svd

# 读取图像
image = cv2.imread('original_image.jpg')

# 将图像转换为灰度图
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 进行SVD分解
U, Sigma, Vh = svd(gray_image, full_matrices=False)

# 截断奇异值
k = 50  # 截断奇异值的数量
Sigma_trunc = Sigma[:k, :k]

# 重构图像
compressed_image = np.dot(U, np.dot(Sigma_trunc, Vh))

# 计算压缩率
compression_ratio = 100 * (1 - compressed_image.size / image.size)

# 保存压缩后的图像
cv2.imwrite('compressed_image.jpg', compressed_image)

print(f'压缩率：{compression_ratio:.2f}%')

**参数说明：**

- `k`：截断奇异值的数量，值越小，压缩率越高，但图像质量损失也越大。

**代码逻辑分析：**

1. 读取图像并转换为灰度图。
2. 对灰度图进行SVD分解，得到奇异值矩阵 `Sigma`。
3. 截断奇异值，保留前 `k` 个奇异值。
4. 使用截断后的奇异值重构图像。
5. 计算压缩率。
6. 保存压缩后的图像。

# 3. SVD在机器学习中的应用

### 3.1 降维

**3.1.1 SVD原理在降维中的应用**

奇异值分解（SVD）是一种强大的降维技术，它可以将高维数据投影到低维空间中，同时保留原始数据中最重要的信息。在机器学习中，降维经常用于：

- 减少特征数量，提高模型的可解释性和训练效率
- 提取数据中的潜在模式和结构
- 去除冗余和噪声，提高模型的泛化能力

SVD将一个矩阵分解为三个矩阵的乘积：

A = UΣV^T

其中：

- **A** 是原始矩阵
- **U** 是左奇异向量矩阵
- **Σ** 是奇异值对角矩阵
- **V** 是右奇异向量矩阵

奇异值对角矩阵中的奇异值表示了原始矩阵中各个特征向量的方差。通过保留最大的奇异值和对应的奇异向量，我们可以将数据投影到一个低维空间中，该空间保留了原始数据中最重要的方差。

### 3.1.2 降维算法的实现

使用SVD进行降维的算法如下：

1. 计算原始矩阵A的奇异值分解：

U, Σ, V = np.linalg.svd(A)

2. 选择要保留的奇异值个数k：

k = 10  # 保留最大的10个奇异值

3. 构造降维后的矩阵：

A_reduced = U[:, :k] @ Σ[:k, :k] @ V[:k, :]

### 3.2 聚类

**3.2.1 SVD原理在聚类中的应用**

聚类是一种将数据点分组为相似组的技术。SVD可以通过以下方式用于聚类：

- 将数据投影到低维空间中，突出数据中的相似性和差异性
- 使用低维投影作为聚类算法的输入，提高聚类效率和准确性

### 3.2.2 聚类算法的实现

使用SVD进行聚类的算法如下：

1. 计算原始矩阵A的奇异值分解：

U, Σ, V = np.linalg.svd(A)

2. 选择要保留的奇异值个数k：

k = 10  # 保留最大的10个奇异值

3. 构造降维后的矩阵：

A_reduced = U[:, :k] @ Σ[:k, :k] @ V[:k, :]

4. 使用聚类算法对降维后的矩阵进行聚类：

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(A_reduced)

5. 根据聚类结果对原始数据进行分组：

cluster_labels = kmeans.labels_

# 4. SVD在自然语言处理中的应用

### 4.1 文本相似度计算

#### 4.1.1 SVD原理在文本相似度计算中的应用

奇异值分解（SVD）在文本相似度计算中发挥着至关重要的作用。SVD将文本表示为一个矩阵，其中行表示文档，列表示单词。通过分解此矩阵，我们可以获得文档之间的相似性度量。

SVD将文本矩阵分解为三个矩阵：U、Σ和V。U矩阵包含文档的左奇异向量，Σ矩阵包含奇异值，V矩阵包含单词的右奇异向量。奇异值表示矩阵中每个奇异向量的重要性。

文本之间的相似性可以通过计算其奇异值分解的余弦相似性来衡量。余弦相似性是两个向量的点积与其范数的乘积之比。对于两个文档A和B，其余弦相似性为：

cos(θ) = (A · B) / (||A|| ||B||)

其中，A · B是A和B的点积，||A||和||B||分别是A和B的范数。

#### 4.1.2 相似度计算算法的实现

使用SVD计算文本相似度的算法如下：

1. **构建文本矩阵：**将文本表示为一个矩阵，其中行表示文档，列表示单词。
2. **计算SVD：**对文本矩阵进行奇异值分解，得到U、Σ和V矩阵。
3. **计算奇异值：**从Σ矩阵中提取奇异值。
4. **计算余弦相似性：**对于每个文档对，计算其奇异值分解的余弦相似性。

### 4.2 文本分类

#### 4.2.1 SVD原理在文本分类中的应用

SVD还可用于文本分类。文本分类的任务是将文本分配到预定义的类别中。SVD通过将文本表示为低维向量来实现这一目标。

通过对文本矩阵进行SVD，我们可以获得一个低秩近似矩阵，其中包含最重要的奇异向量。这个低秩近似矩阵可以用来表示文本的语义信息。

#### 4.2.2 分类算法的实现

使用SVD进行文本分类的算法如下：

1. **构建文本矩阵：**将文本表示为一个矩阵，其中行表示文档，列表示单词。
2. **计算SVD：**对文本矩阵进行奇异值分解，得到U、Σ和V矩阵。
3. **提取低秩近似矩阵：**从U和Σ矩阵中提取低秩近似矩阵。
4. **使用分类器：**使用分类器（如支持向量机或逻辑回归）对低秩近似矩阵进行训练。
5. **分类新文本：**将新文本表示为低秩近似矩阵，并使用训练好的分类器对其进行分类。

# 5.1 SVD在推荐系统中的应用

### 5.1.1 SVD原理在推荐系统中的应用

奇异值分解（SVD）在推荐系统中扮演着至关重要的角色，因为它可以将用户-物品交互矩阵分解为三个矩阵：用户矩阵、奇异值矩阵和物品矩阵。

* **用户矩阵：**表示每个用户对每个物品的喜好程度。
* **奇异值矩阵：**包含奇异值，表示用户和物品之间的相似性。
* **物品矩阵：**表示每个物品的特征。

通过对用户-物品交互矩阵进行SVD分解，我们可以获得用户的潜在特征和物品的潜在特征，从而可以对用户进行聚类，并根据用户的喜好为他们推荐物品。

### 5.1.2 推荐算法的实现

基于SVD的推荐算法通常遵循以下步骤：

1. **数据准备：**收集用户-物品交互数据，并将其转换为用户-物品矩阵。
2. **SVD分解：**对用户-物品矩阵进行SVD分解，得到用户矩阵、奇异值矩阵和物品矩阵。
3. **用户聚类：**根据用户矩阵对用户进行聚类，将具有相似喜好的用户分组。
4. **物品推荐：**对于每个用户，根据其所属的簇和物品矩阵，为其推荐与簇内其他用户喜好相似的物品。

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 加载用户-物品交互数据
data = np.loadtxt('user_item_interactions.csv', delimiter=',')

# 创建用户-物品矩阵
user_item_matrix = data.reshape((data.shape[0], -1))

# 进行SVD分解
svd = TruncatedSVD(n_components=10)
svd.fit(user_item_matrix)

# 获取用户矩阵、奇异值矩阵和物品矩阵
user_matrix = svd.components_
singular_values = svd.singular_values_
item_matrix = svd.transform(user_item_matrix)

# 对用户进行聚类
from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=5)
kmeans.fit(user_matrix)

# 为每个用户推荐物品
for user_id in range(user_item_matrix.shape[0]):
    cluster_id = kmeans.labels_[user_id]
    similar_users = np.where(kmeans.labels_ == cluster_id)[0]
    recommended_items = item_matrix[similar_users, :].mean(axis=0)