【基础】牛顿法的介绍及Matlab实现

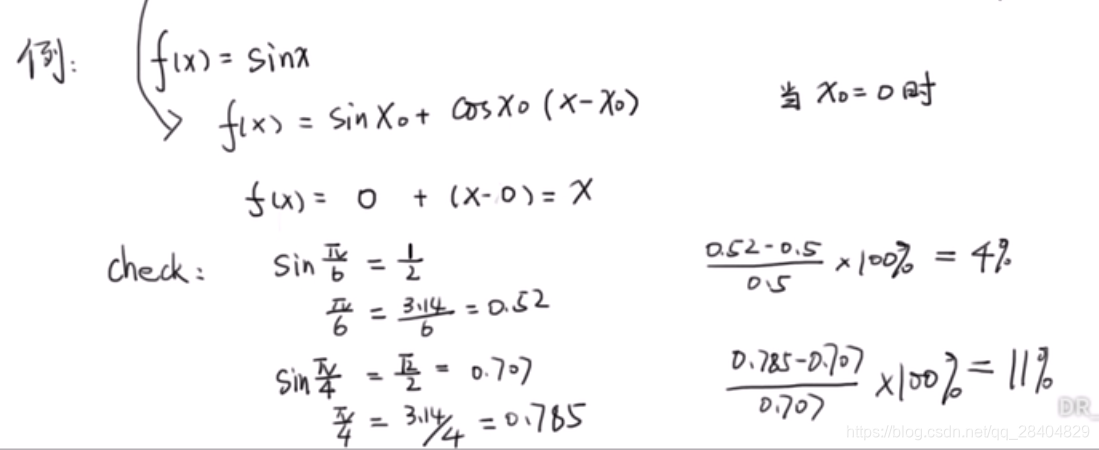
# 1. 牛顿法的理论基础**

牛顿法，又称切线法，是一种求解非线性方程的迭代方法。其基本思想是：对于给定的非线性方程 f(x) = 0，在初始点 x0 处作 f(x) 的切线，并求出切线与 x 轴的交点 x1。然后以 x1 为新的初始点，重复上述过程，直到满足一定的终止条件。

牛顿法的迭代公式为：

x_{n+1} = x_n - f(x_n) / f'(x_n)

其中：

* x_n 是第 n 次迭代的近似值
* f(x_n) 是 f(x) 在 x_n 处的函数值
* f'(x_n) 是 f(x) 在 x_n 处的导数值

# 2. 牛顿法在Matlab中的实现

### 2.1 牛顿法算法的Matlab代码

牛顿法算法的Matlab代码主要包括两个部分：牛顿法方程的求解和导数的计算。

#### 2.1.1 牛顿法方程的求解

function x = newton_method(f, df, x0, tol, max_iter)
% 牛顿法求解方程
% 输入：
%   f: 方程函数
%   df: 方程导数函数
%   x0: 初始猜测值
%   tol: 容差
%   max_iter: 最大迭代次数
% 输出：
%   x: 求得的根

% 初始化
x = x0;
iter = 0;

% 迭代求解
while iter < max_iter && abs(f(x)) > tol
    x = x - f(x) / df(x);
    iter = iter + 1;
end

% 判断是否收敛
if iter == max_iter
    warning('牛顿法未收敛，达到最大迭代次数。');
end
end

**代码逻辑分析：**

* 函数`newton_method`接受方程函数`f`、导数函数`df`、初始猜测值`x0`、容差`tol`和最大迭代次数`max_iter`作为输入，返回求得的根`x`。
* 函数首先初始化`x`为`x0`，并设置迭代次数`iter`为0。
* 进入迭代循环，在循环中使用牛顿法迭代公式更新`x`的值，并递增`iter`。
* 循环条件为`iter`小于`max_iter`且方程值`f(x)`的绝对值大于`tol`。
* 如果迭代次数达到`max_iter`，则发出警告，表示牛顿法未收敛。

#### 2.1.2 导数的计算

function df = derivative(f, x)
% 计算函数的导数
% 输入：
%   f: 函数
%   x: 自变量
% 输出：
%   df: 导数值

% 数值微分
h = 1e-6;
df = (f(x + h) - f(x)) / h;
end

**代码逻辑分析：**

* 函数`derivative`接受函数`f`和自变量`x`作为输入，返回导数值`df`。
* 函数使用数值微分方法计算导数，通过计算函数在`x`附近的一个小增量`h`处的差值来近似导数。
* 数值微分方法简单易用，但精度有限，尤其是在函数变化剧烈或存在噪声时。

### 2.2 牛顿法收敛性的分析

#### 2.2.1 收敛条件

牛顿法收敛的充分条件是方程在根的邻域内满足以下条件：

* 方程二阶导数不为零。
* 方程三阶导数存在且有界。

#### 2.2.2 收敛速度

牛顿法的收敛速度与方程的二阶导数有关。如果二阶导数在根的邻域内保持正（负），则牛顿法将以二次（超二次）速度收敛。

# 3. 牛顿法在Matlab中的应用**

**3.1 多项式方程的求解**

牛顿法在求解多项式