【实战演练】MATLAB实现tsp（旅行商问题） 利用matlab遗传算法、模拟退火算法以及lingo动态规划求解

# 2.1.1 遗传算法的基本原理

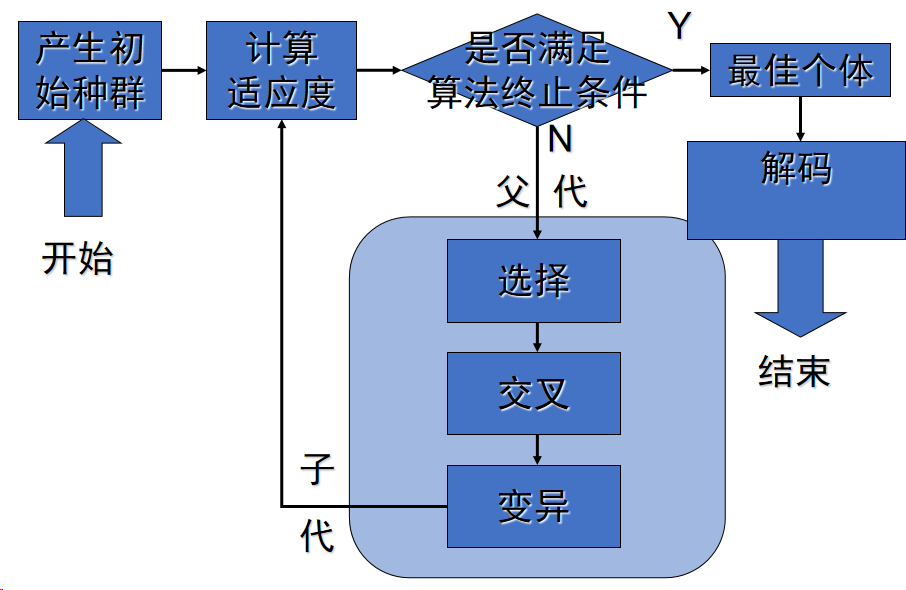
遗传算法（GA）是一种受生物进化过程启发的优化算法。它通过模拟自然选择和遗传变异来寻找问题的最优解。GA的流程如下：

1. **初始化种群：**随机生成一组候选解，称为种群。
2. **评估种群：**计算每个个体的适应度，即其解决问题的优劣程度。
3. **选择：**根据适应度选择种群中较好的个体进行繁殖。
4. **交叉：**将选定的个体配对并交换基因，产生新的个体。
5. **变异：**随机改变新个体的基因，引入多样性。
6. **重复步骤2-5：**直到满足终止条件（例如达到最大迭代次数或找到足够好的解）。

# 2. MATLAB中TSP算法实现

### 2.1 遗传算法

#### 2.1.1 遗传算法的基本原理

遗传算法（GA）是一种受生物进化过程启发的优化算法。它通过模拟自然选择和遗传过程，从一组候选解（称为种群）中迭代生成更好的解。GA的基本原理如下：

* **初始化种群：**随机生成一组候选解，每个解表示一个可能的TSP解决方案。
* **适应度评估：**计算每个解的适应度，即其解决TSP问题的能力。
* **选择：**根据适应度选择种群中的个体进行繁殖，适应度较高的个体更有可能被选中。
* **交叉：**将两个选定的个体的遗传信息（即解决方案）结合起来，产生新的个体。
* **变异：**对新个体进行随机修改，以引入多样性并防止算法陷入局部最优解。
* **迭代：**重复选择、交叉和变异步骤，直到达到停止条件（例如，达到最大迭代次数或找到满足要求的解决方案）。

#### 2.1.2 MATLAB中遗传算法的实现

MATLAB中可以使用`ga`函数实现遗传算法。该函数接受以下参数：

* `FitnessFunction`：适应度函数，用于计算每个解的适应度。
* `nvars`：变量数，即TSP中城市的个数。
* `options`：算法选项，包括种群大小、最大迭代次数等。

% 定义适应度函数
fitnessFunction = @(x) tspfun(x);

% 定义算法选项
options = gaoptimset('PopulationSize', 100, 'MaxGenerations', 100);

% 执行遗传算法
[x, fval, exitflag, output] = ga(fitnessFunction, nvars, [], [], [], [], [], [], [], options);

### 2.2 模拟退火算法

#### 2.2.1 模拟退火算法的基本原理

模拟退火算法（SA）是一种受金属退火过程启发的优化算法。它通过逐渐降低算法的温度，从一个初始解出发，逐步搜索更好的解。SA的基本原理如下：

* **初始化：**从一个随机解开始，并设置一个初始温度。
* **扰动：**随机生成一个新的解，并计算其适应度。
* **接受准则：**如果新解比当前解好，则接受它。如果新解比当前解差，则以一定概率接受它，该概率随着温度的降低而减小。
* **温度更新：**在每次迭代中，降低温度，以减少接受差解的概率。
* **迭代：**重复扰动、接受准则和温度更新步骤，直到达到停止条件。

#### 2.2.2 MATLAB中模拟退火算法的实现

MATLAB中可以使用`simulannealbnd`函数实现模拟退火算法。该函数接受以下参数：

* `fun`：目标函数，用于计算每个解的适应度。
* `bounds`：变量的边界，即TSP中城市的位置范围。
* `options`：算法选项，包括初始温度、冷却速率等。

% 定义目标函数
fun = @(x) tspfun(x);

% 定义变量边界
bounds = [0, 100; 0, 100];

% 定义算法选项
options = simulannealbnd(fun, bounds, options);

% 执行模拟退火算法
[x, fval, exitflag, output] = simulannealbnd(fun, bounds, options);

### 2.3 动态规划算法

#### 2.3.1 动态规划算法的基本原理

动态规划算法（DP）是一种通过将问题分解成较小的子问题，并逐步求解这些子问题，从而解决复杂问题的算法。对于TSP，DP的基本原理如下：

* **定义子问题：**对于TSP中的每个城市，定义一个子问题，即从该城市出发，访问所有其他城市并返回该城市的最小距离。
* **建立状态转移方程：**对于每个子问题，建立一个状态转移方程，该方程描述了如何使用已求解的子问题的解来求解当前子问题。
* **递归求解：**从最