深度学习中的不确定性：贝叶斯神经网络教程

"这篇文档是Wesley Maddox关于贝叶斯神经网络的教程，旨在帮助机器学习和深度学习的研究者理解并应用贝叶斯统计来量化深度神经网络的预测不确定性。文档涵盖了从动机到具体实现方法的全面内容，包括贝叶斯推断的基本原理、近似推理、变分推理、拉普拉斯近似、马尔科夫链蒙特卡洛（MCMC）方法以及由损失几何启发的方法（作者的工作）。文档还通过实例展示了在深度学习中不确定性的重要性，如自动驾驶中的不可见攻击和医疗诊断中的可信度校准问题。" **贝叶斯神经网络（Bayesian Neural Networks, BNNs）** 贝叶斯神经网络是一种结合了贝叶斯统计理论的深度学习模型。在传统神经网络中，参数（权重和偏置）通常是确定性的，而在BNNs中，这些参数被视为随机变量，具有概率分布。这种处理方式使得BNNs能够提供关于预测的不确定性估计，这对于许多现实世界的应用，如医疗诊断和自动驾驶，至关重要。 **动机** 深度学习在许多领域取得了显著成功，但其预测的黑箱特性限制了对模型不确定性的理解。BNNs提供了一种框架，可以量化模型预测的不确定性，从而提高模型的可靠性。例如，在医疗诊断中，当模型对病人的病情预测具有高置信度时，BNNs可以给出健康和不健康状态的精确概率，这有助于医生作出决策。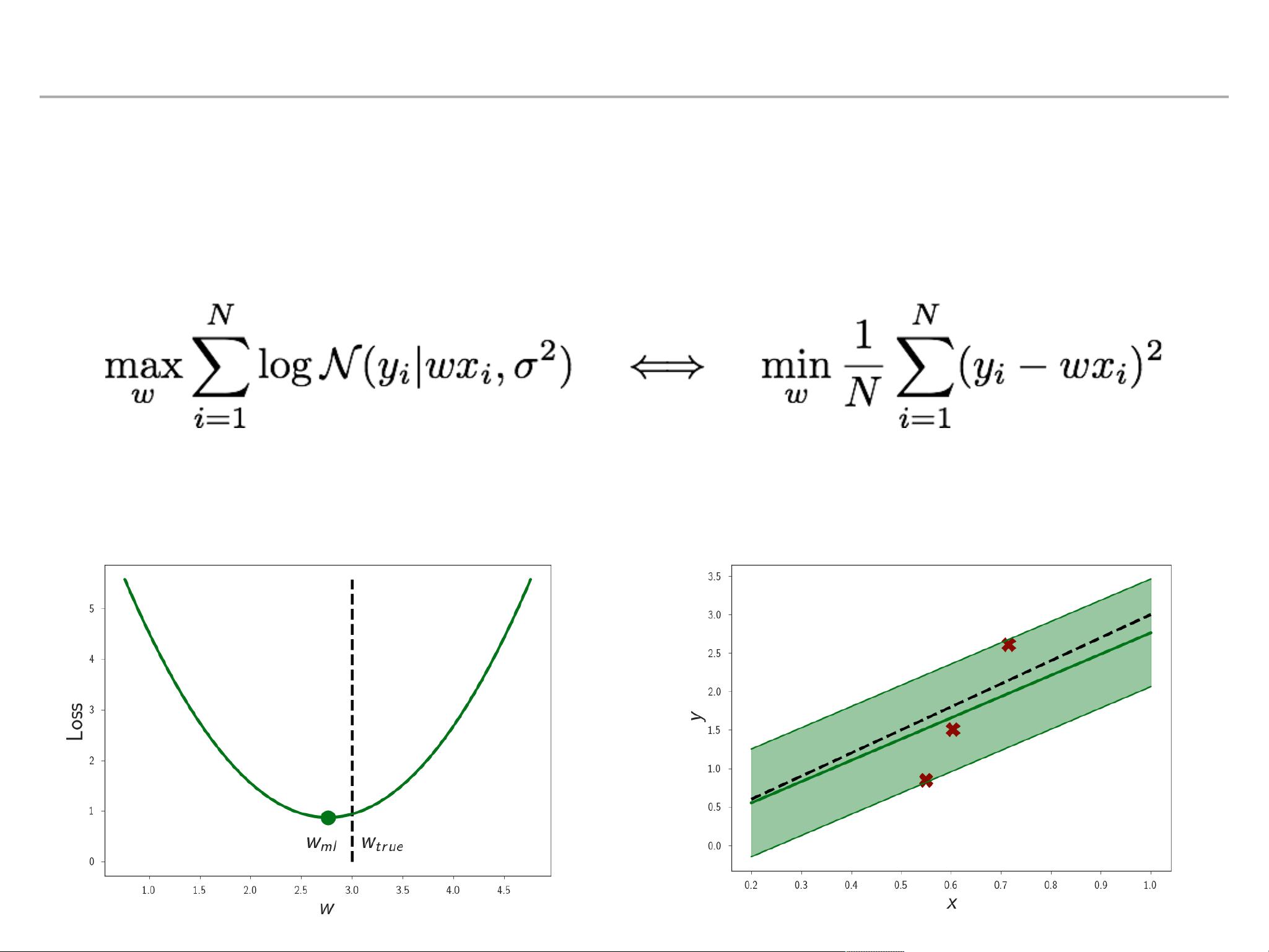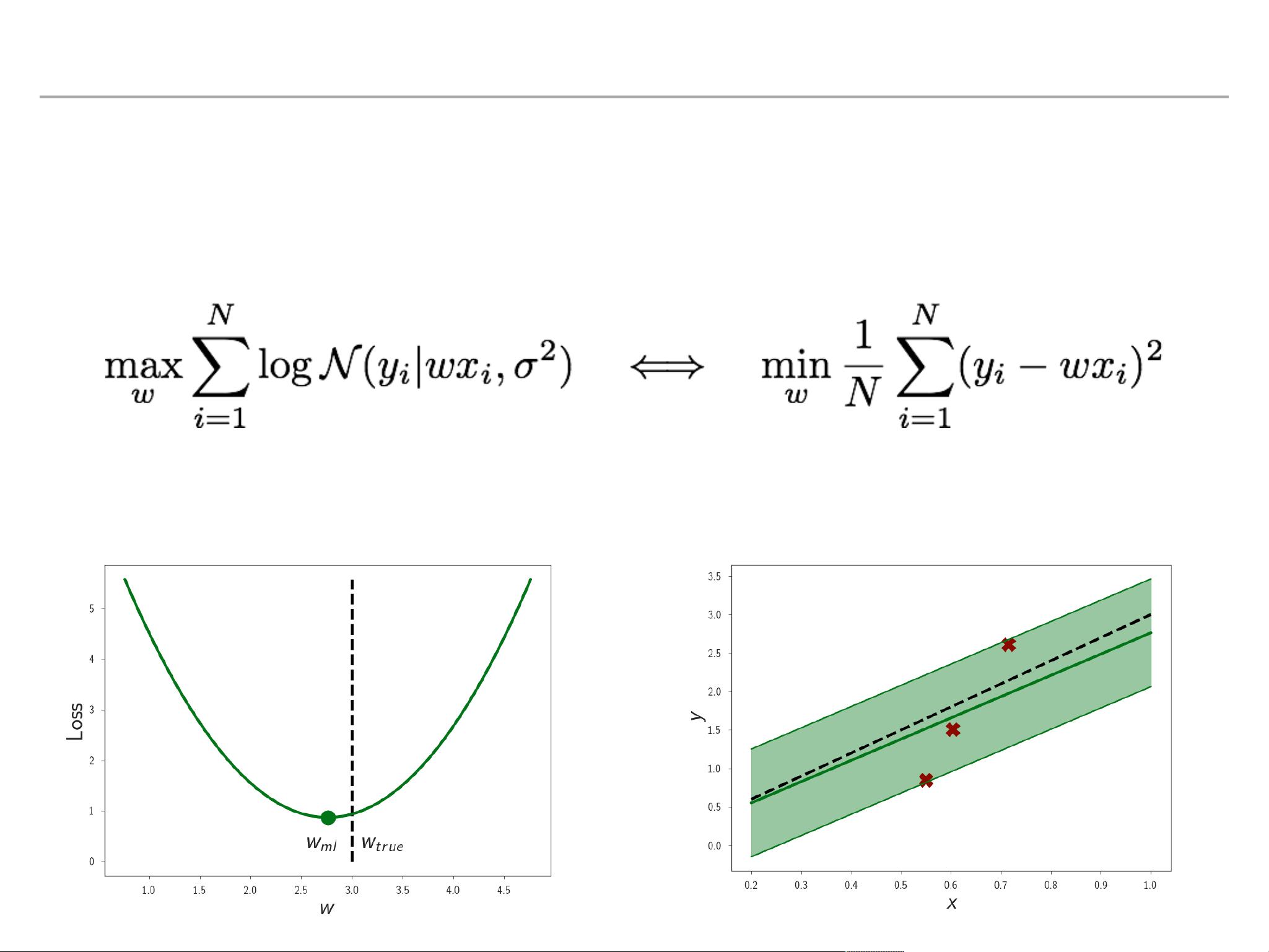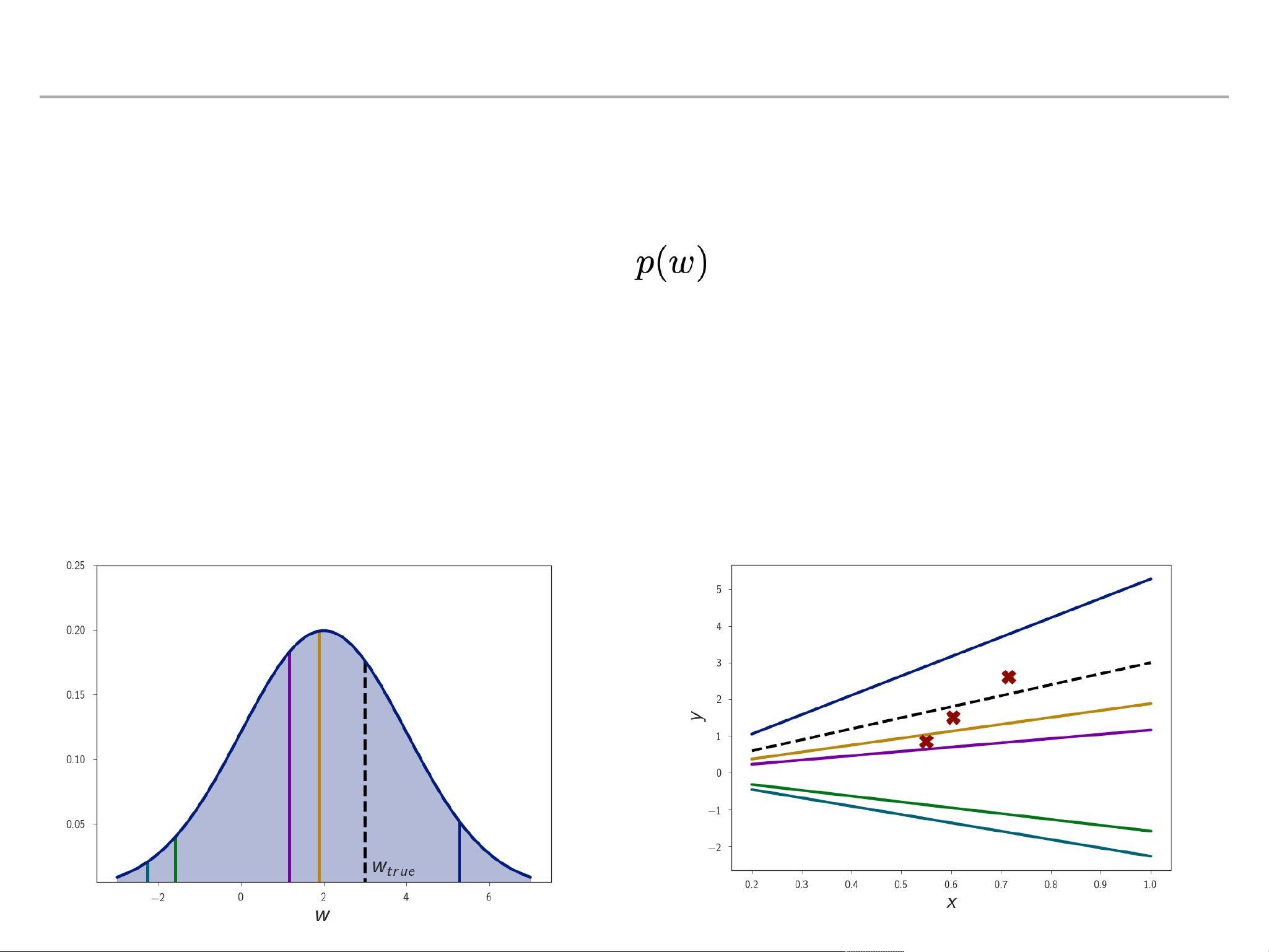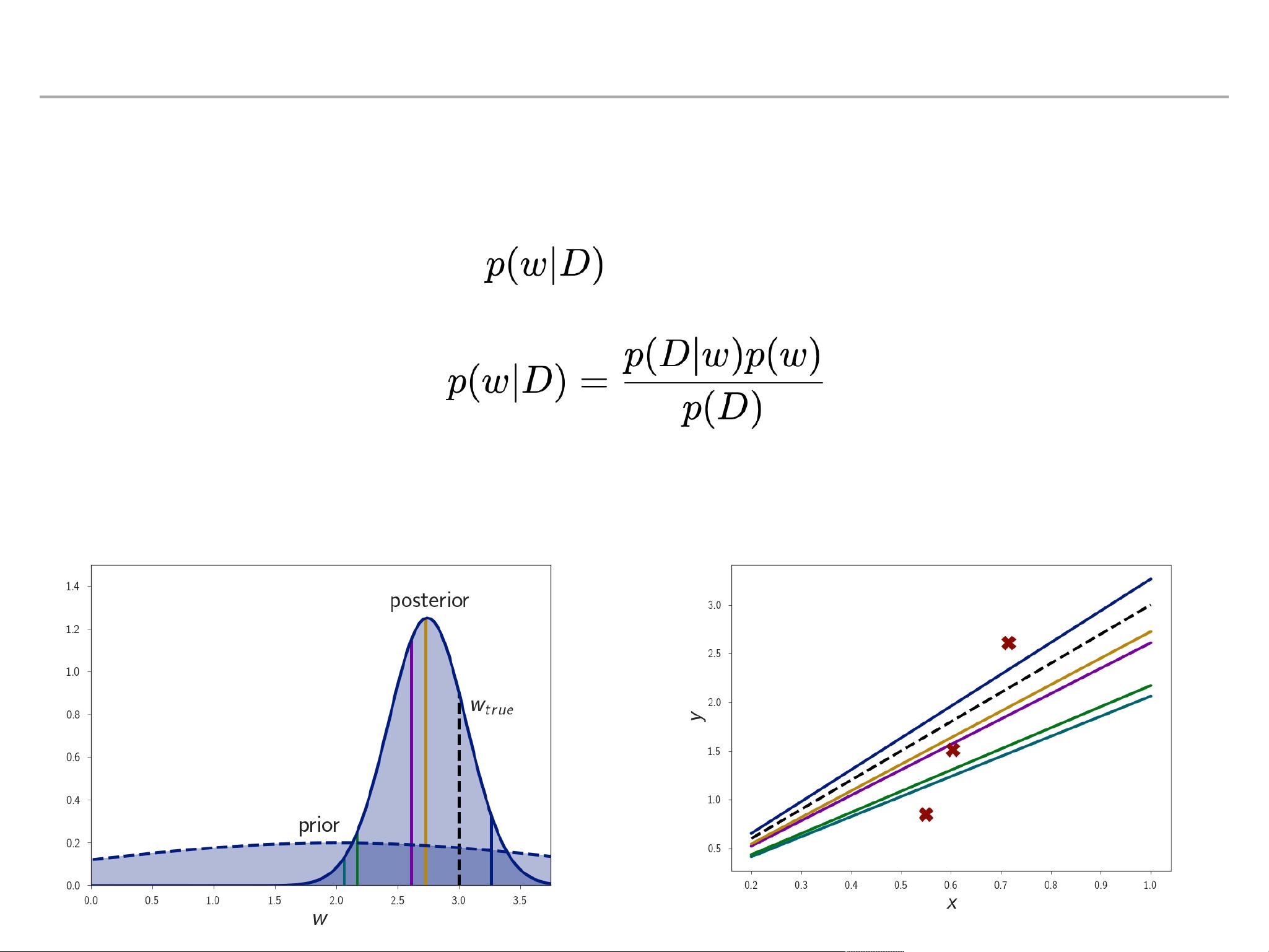 **贝叶斯推断** 贝叶斯推断是估计未知参数的概率分布的方法，它允许我们更新我们的信念（先验概率）随着新数据（观测值）的出现（后验概率）。在BNNs中，这个过程涉及到对网络参数的分布进行采样，以获得多个可能的模型，每个模型代表一种不同的预测结果。 **近似推理** 由于完全的贝叶斯推断在大型神经网络中通常是计算上不可行的，因此需要使用近似方法。常见的近似方法包括变分推理（Variational Inference, VI），它通过最小化后验分布和一个易于操作的近似分布之间的差距来估计参数分布。另一种方法是拉普拉斯近似，通过找到梯度的零点来近似后验的峰值。 **马尔科夫链蒙特卡洛（MCMC）** MCMC是一种采样技术，用于在高维空间中生成后验分布的样本。虽然MCMC方法可以提供更准确的后验估计，但它们通常需要大量的计算资源和时间。 **损失几何启发的方法** 作者的工作集中在利用损失函数的几何特性来改进近似推理。这些方法可能包括优化过程中的策略调整或对损失空间的深入分析，以提高BNNs的性能和不确定性估计的准确性。 **不确定性在深度学习中的重要性** 文档中提到的实例强调了不确定性估计在深度学习中的必要性。例如，自动驾驶系统需要能够识别和应对潜在的攻击，而医疗诊断系统则需要提供可信度校准的预测，确保模型在给出高置信度预测时实际上是正确的。 贝叶斯神经网络提供了一个强大而严谨的框架，以理解和量化深度学习模型的不确定性。通过理解和应用BNNs，研究者和工程师可以构建出更加可靠和透明的模型，这对那些要求高精度和可解释性的应用来说是至关重要的。