小波变换深入解析：从理论到应用实践

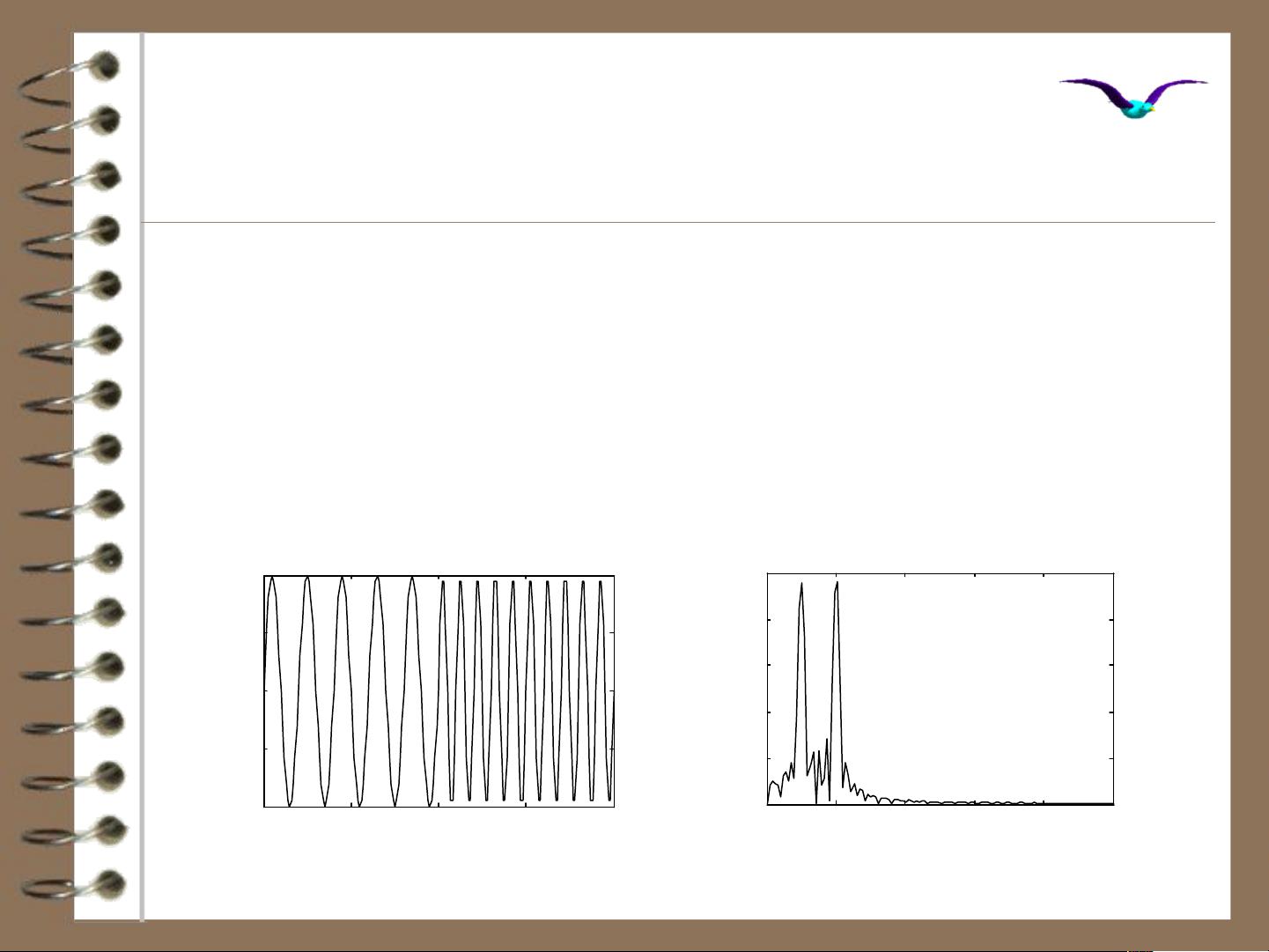
"小波变换的原理与应用" 小波变换是一种强大的数学工具，它结合了傅里叶变换的时间频率分析特性与局部化优势，能够同时在时域和频域中提供信息。小波变换的发展历程可以追溯到1909年，由Alfred Haar提出的第一种小波——Haar小波。然而，真正推动小波分析进入主流领域的是1980年代，尤其是J.Morlet提出的小波变换概念，以及后续Y.Meyer构建的正交小波基和S.Mallat的快速算法。 小波变换与傅里叶变换相比，有其独特之处。傅里叶变换将信号转换为频域表示，揭示了信号的频率成分，但无法获取信号的精确时间信息。而小波变换则利用“时间-频率”窗口来分析信号，这种窗口可以移动和缩放，因此能捕捉到信号的局部特征，对于非平稳信号的分析尤其有用。 小波变换的基本原理涉及尺度和翻译操作。通过调整小波函数的尺度（频率）和位置（时间），可以适应不同频率和时间尺度的信号特性。这使得小波变换能够对信号进行多分辨率分析，从而更准确地识别信号的突变和局部特征。 常用的小波有多种，例如Morlet小波、Daubechies小波等。Morlet小波是最早被广泛使用的小波之一，具有良好的频率分辨率和时间定位。Daubechies小波由Inrid Daubechies提出，它们是一组具有有限支撑的正交小波，适用于离散小波分析，特别适用于信号压缩和去噪。 小波变换的应用广泛，特别是在图像处理中，它可以用于图像的压缩、去噪和特征提取。例如，在图像去噪应用中，小波变换能够有效地分离信号与噪声，通过阈值处理去除高频噪声，同时保留图像的细节信息。此外，小波分析在语音信号处理、医学信号分析（如心电信号分析）等领域也有广泛应用。 尽管小波变换在很多方面都表现优秀，但仍存在一些挑战。例如，选择合适的小波基、计算复杂性、以及处理非线性、非stationary信号的有效方法等。随着研究的深入，这些问题逐渐得到解决，小波分析的潜力也在不断被挖掘，未来在更多领域有着广阔的应用前景。