山东大学软件学院机器学习实验：三维数据的Gaussian MLE估计与比较

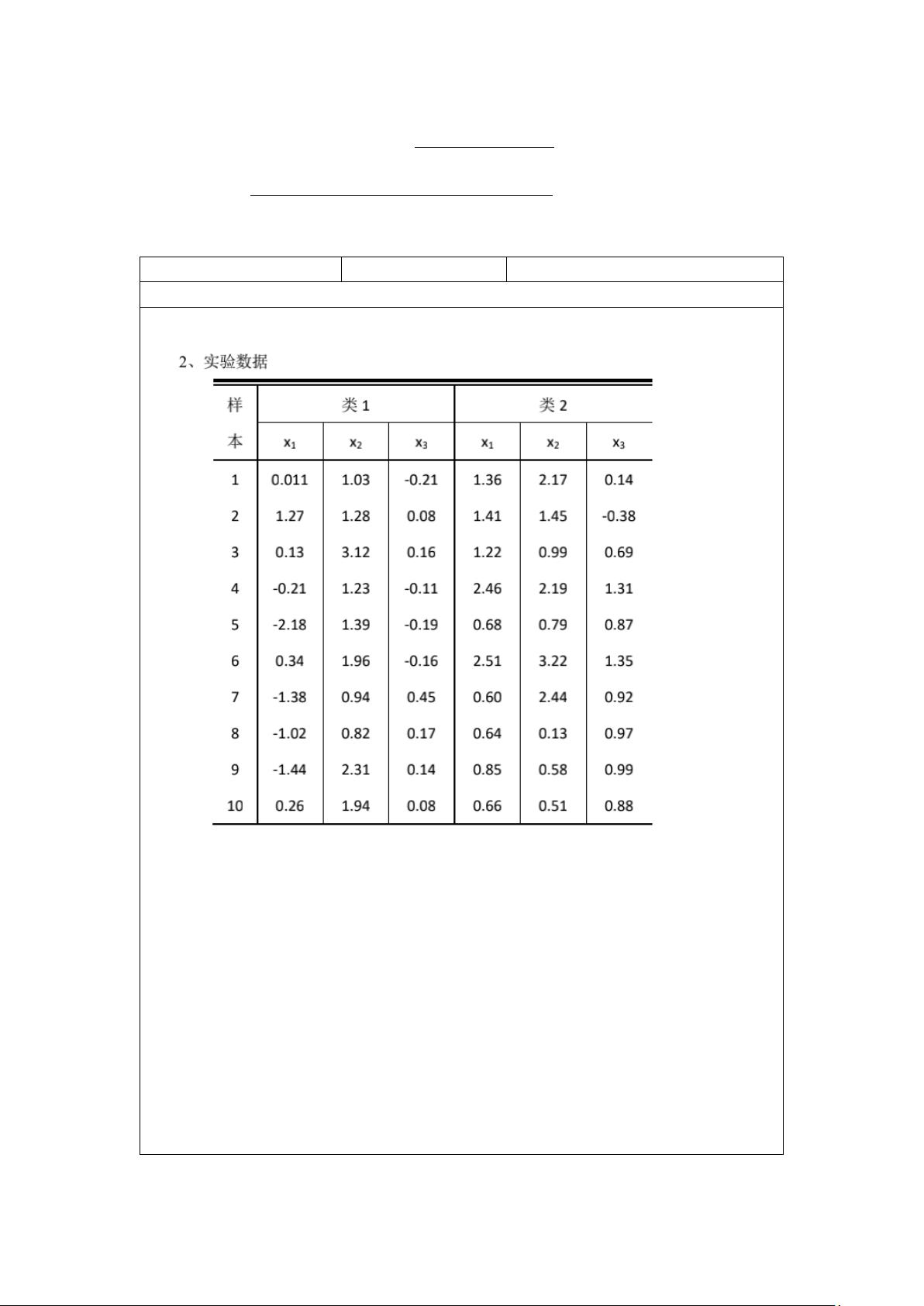
本实验主要涉及机器学习中的概率模型估计和数据分析，针对山东大学软件学院的一名学生傅显坤（学号201800301153）进行的课程实验。实验内容主要包括以下几个部分： 1. **二维数据处理**： 实验要求编写程序，处理二维数据的概率分布$p(\mathbf{x}) \sim N(\boldsymbol{\mu}, \boldsymbol{\Sigma})$，对于类1和类2中的任意两个特征的组合，分别求解最大似然估计的均值$\boldsymbol{\mu}^\#$和方差$\boldsymbol{\Sigma}^\#$。这涉及到统计推断和优化方法，通过观察不同特征组合的参数估计，可以分析数据的联合分布特性。 2. **三维数据处理**： 进一步扩展到三维数据($\mathbf{x}$)的处理，同样基于高斯分布$N(\boldsymbol{\mu}, \boldsymbol{\Sigma})$，需估计类1和类2中三个特征的最大似然估计均值$\boldsymbol{\mu}^\#$和方差$\boldsymbol{\Sigma}^\#$。这要求对多维数据的数学建模和计算能力有深入理解。 3. **高斯模型的可分性**： 假设三维高斯模型的协方差矩阵是分离的，即$\boldsymbol{\Sigma} = \text{diag}(\sigma_{12}, \sigma_{22}, \sigma_{32})$，学生被要求编写程序来估计类1和类2的均值和各个特征间的独立方差参数。这涉及到高斯分布的特殊结构在模型拟合上的应用。 4. **参数比较与解释**： 实验还要求对比前三种方法（二维和三维数据的高斯分布参数估计）计算出的特征均值$\mu_i$和方差$\sigma_i$的异同，并提供合理的解释。这涉及到对不同数据维度下参数估计稳定性和模型适用性的评估。 这个实验涵盖了机器学习中的基础统计建模、参数估计和模型验证技巧，要求学生具备编程实现统计模型、理解和应用最大似然估计，以及数据可视化和解释结果的能力。通过实践，学生能深化对多元高斯分布的理解，并提升实际问题解决的能力。