1/2 BPS Wilson环上的缺陷变换算子结构常数解析

25 浏览量更新于2024-07-16 收藏 746KB PDF 举报

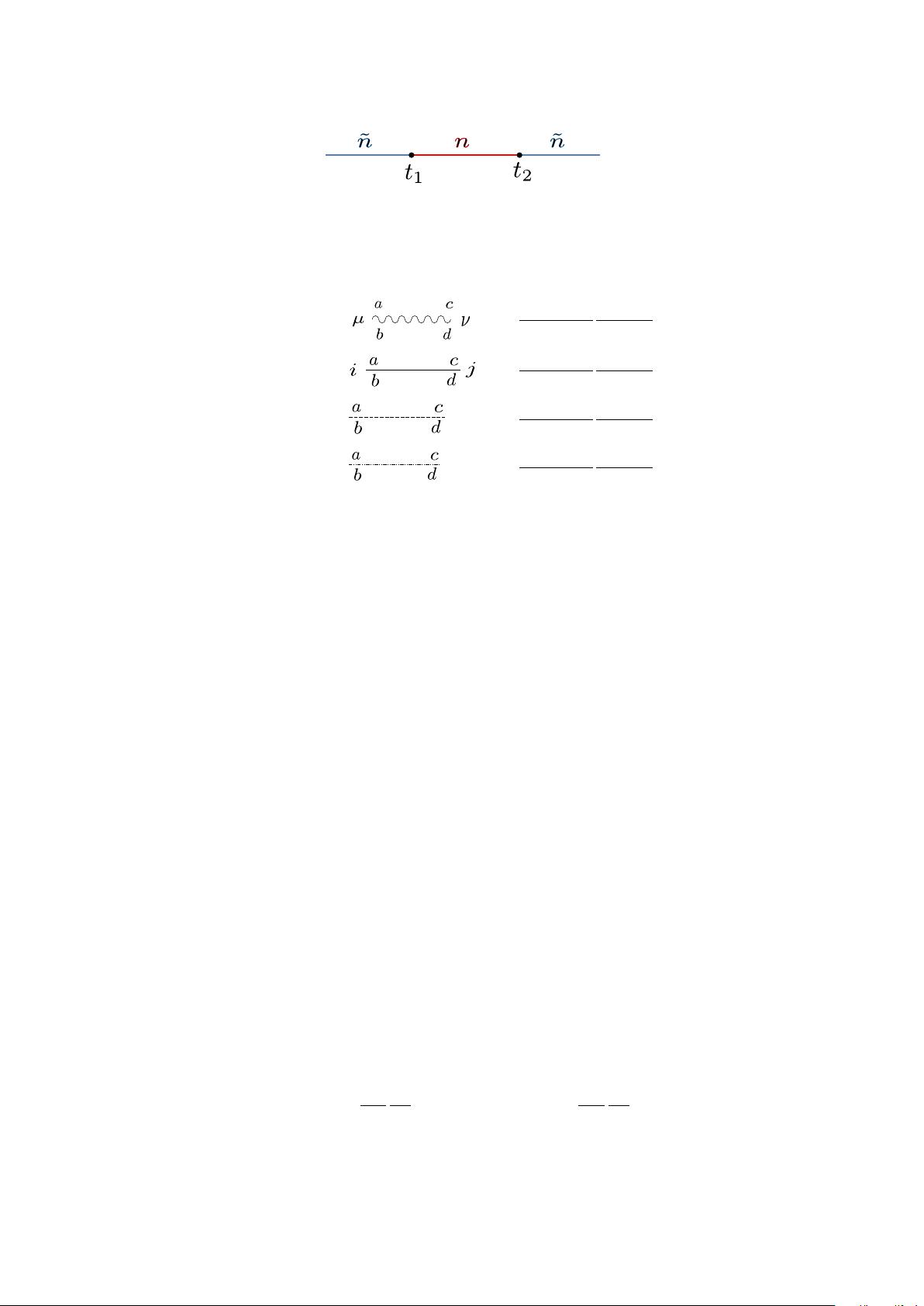
本文主要探讨的是1/2 BPS Wilson环在平面N=4超杨-米尔斯理论中的缺陷改变算子的三点函数。在N=4超杨-米尔斯理论这个高能物理学的背景下，1/2 BPS Wilson环是一种重要的非perturbative对象，它代表了一种特定类型的闭合路径，其在量子场论中具有深刻的物理意义，特别是与AdS/CFT对应关系中的几何形状。 "缺陷改变算子"是本文的核心关注点，它们的作用是改变与Wilson环耦合的标量场的性质。这种算子在量子场论中的作用类似于在弦理论或缺陷凝聚态系统中的"缺陷"，它们可以扰动系统的对称性和局部性质。作者们首先在一般设置下对两个这样的1/2 BPS Wilson环上的算子三点函数进行了计算，这涉及到了复杂的量子场论计算，包括对费曼图的分析。接着，他们特别关注了一个被称为"梯形极限"的特殊情况，这是一个特殊的缩放比例极限，在这个极限下，系统的光谱被精确地描述为SL(2, ℝ)对称性下的量子力学模型。这种对称性的存在使得问题变得更为简化，使得理论的解析解成为可能。利用Schwinger-Dyson方程，他们能够重构出所有阶数的结构常数，这些常数是衡量三个算子相互作用强度的重要物理量。值得注意的是，这些结果不仅提供了一个关于缺陷共形场理论的可解决模型的示例，而且还为基于可积性方法计算结构常数的研究提供了宝贵的实证数据。文章《JHEP12(2017)055》发表于Springer，是开放获取的，这意味着学术界的研究人员可以自由访问和利用这些成果。作者们来自多个知名机构，他们的工作揭示了1/2 BPS Wilson环上的算子相互作用在理论层面上的深刻见解，这对于理解超对称场论的量子行为以及可能的量子引力效应具有重要意义。总结来说，这篇论文深入研究了1/2 BPS Wilson环上的缺陷改变算子的结构常数，展示了理论物理学家如何通过精细的计算和特殊极限来探索这些复杂系统的非平凡性质，同时为后续的理论研究和数值模拟提供了有价值的数据和参考框架。

JHEP12(2017)055

Figure 2. Two-point function of defect changing operators.

Using this action, one can compute the propagators as follows:

Gluon : =

8π

µν

|x − y|

Scalar : =

8π

|x − y|

Fermion : =

8π

|x − y|

Ghost : =

8π

|x − y|

(2.15)

Here a-d are the color indices and all the propagators are proportional to δ

. To compute

the loop corrections, one just need to bring down the interaction terms by expanding e

−S

and Wick-contract the ﬁelds using the propagators.

3 Two-point functions at two loops

Let us ﬁrst compute the two-point function of defect changing operators at two loops. The

purpose of this section is twofold; to reproduce the anomalous dimension known in the liter-

ature and to determine the normalization of the operator, which is necessary for extracting

the scheme-independent structure constant from perturbative three-point functions.

3.1 One loop

The two-point function we compute is of the following form (see also ﬁgure 2):

hW [O

)]i ≡





Pexp



−∞

dτ iA

˙x

+ φ

˜n

|˙x



Pexp



dτ iA

˙x

+ φ

|˙x



Pexp



∞

dτ iA

˙x

+ φ

˜n

|˙x



(3.1)

Owing to the SO(6) invariance, it only depends on the inner product n · ˜n and the cou-

pling constant λ. To perform the perturbative computation, we just need to expand the

exponentials in (3.1) and contract them with propagators and vertices.

At one loop, one can only have a single propagator (without vertices). The propagator

can be either a gauge ﬁeld or a scalar ﬁeld and takes the form,

Gauge : −

8π

, Scalar : (n

· n

)

8π

, (3.2)

– 6 –

JHEP12(2017)055

Figure 3. One-loop corrections to the two-point function of defect changing operators. Owing to

the cancellation between gluons and scalars, the only diagrams that survive are the ones in which

the propagator connects two diﬀerent segments.

where τ

= τ

− τ

is the distance between two end points and n

and n

(which can be

either n or ˜n) are the polarization vectors at each end point. The extra minus sign for

gluons comes from factors of i in the exponentials in (3.1). As is clear from (3.2), the

contributions from the gauge ﬁeld and the scalar ﬁeld cancel out if n

= n

, since both n

and ˜n have a unit norm. We are thus left with diagrams in which a propagator connects

two segments with diﬀerent polarizations (see ﬁgure 3).

To compute such diagrams, we introduce a UV regularization by cutting out a small

circle of radius

/2 around each operator. This leads to a regularized integral

hW [O

)]i

1-loop

λ(n · ˜n − 1)

8π

−

−∞

dτ

−

dτ

−

dτ

∞

dτ

(3.3)

with t

= t

± /2. This integral can be easily evaluated using

dτ

= log

(a − c)(b − d)

(a − d)(b − c)

, (3.4)

hW [O

)]i

1-loop

λ(n · ˜n − 1)

4π

log



+ O() . (3.5)

Comparing this with (2.7), we can determine the one-loop normalization a

(1)

and the

anomalous dimension γ

(1)

= 0 , γ

(1)

1 − n · ˜n

8π

. (3.6)

The result for γ

(1)

of course matches the one in the literature [13], but it also shows that

the normalization at one loop a

(1)

vanishes in our scheme.

3.2 Two loops

Let us now proceed to the two-loop computation. At two loops, there appear three types

of diagrams; the ladder, the vertex and the self-energy. Below we are going to evaluate

them one by one.

Ladder diagrams. The ﬁrst diagrams are the ladder diagrams, which consist only of

propagators. For this class of diagrams, the computation proceeds in a similar manner as

in the previous subsection. Also here, the diagrams that contain propagators connecting

the same segment vanish due to the cancellation between the scalar and the gluon.

The factor of 1/2 is just a useful convention which simpliﬁes the ﬁnal result.

– 7 –

剩余38页未读，继续阅读

weixin_38639872

粉丝: 9
资源: 952

1/2 BPS Wilson环上的缺陷变换算子结构常数解析

N = 4 $$ \ mathcal {N} = 4 $$ Chern-Simons-matter理论中大量的1/2 BPS Wilson循环

N = 4 $$ \ mathcal {N} = 4 $$ Chern-Simons-matter理论中的量子1/2 BPS Wilson循环

ABJM理论中1/6 BPS Wilson循环的瞬时校正

AdS5×S5中1/4 BPS Wilson环的1环弦修正微扰计算

1/4 BPS Wilson-t Hooft环在N=4 SYM中的电磁对称性与守恒量计算

在大约1/4 BPS的Wilson-t Hooft循环中

半BPS Wilson循环和AdS 2 / CFT 1

注意在<math> <mi> N </ mi> </ math> $$ \ mathcal {N} $$ = 4 SYM理论中生成1 / 2-BPS Wilson循环的函数和相关的相关器

AdS 5×S 5中1 / 4-BPS Wilson环的精度计算

关于ABJM中多伤口BPS Wilson循环的注释

最新资源