一元稀疏多项式简单计算器-多项式加法乘法实验报告

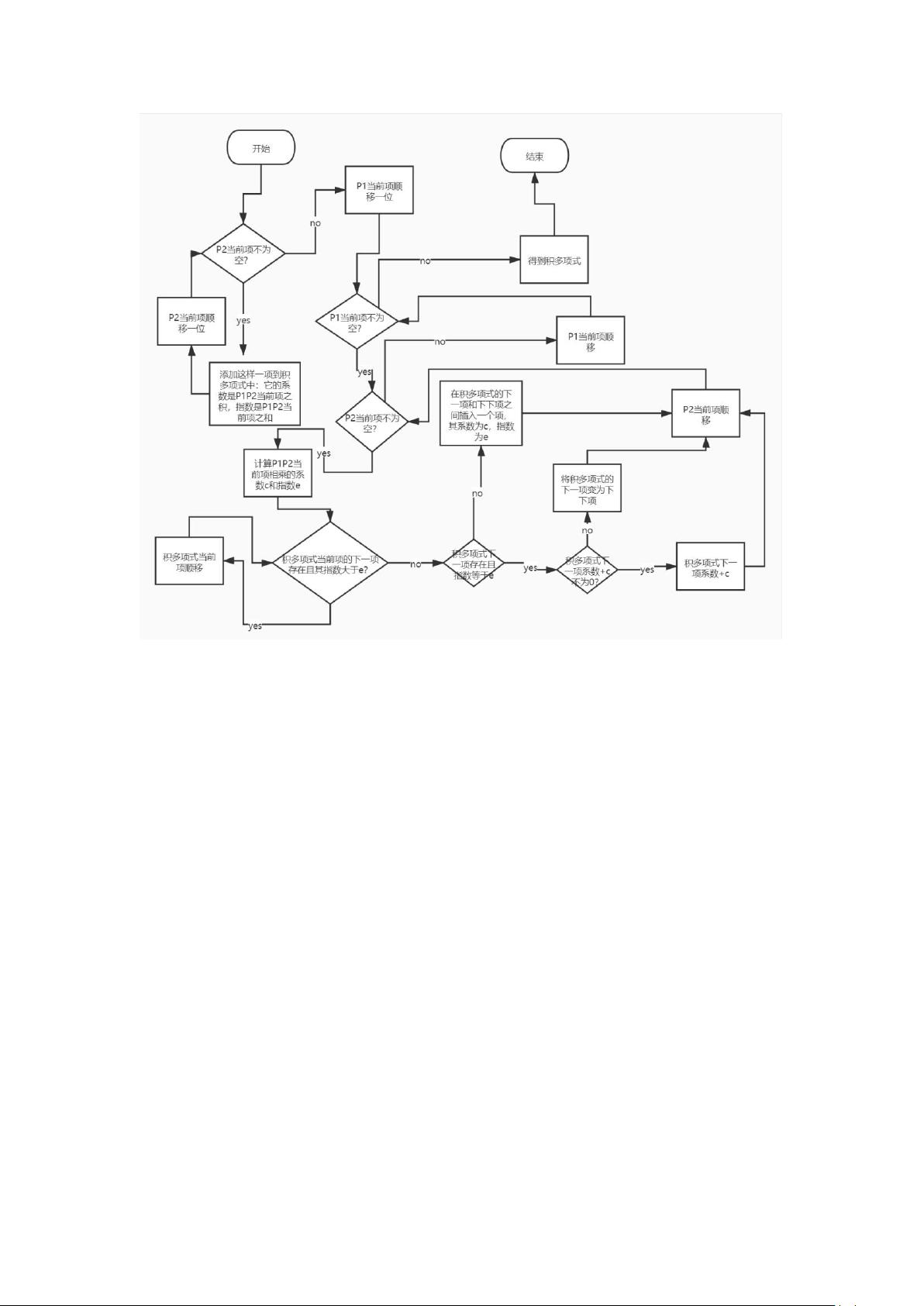
实验报告：多项式加法乘法问题 实验目的： 本实验的目的是设计一个一元稀疏多项式简单计算器，实现多项式的加法和乘法运算。 实验内容与要求： 1. 输入并建立多项式。 2. 输出多项式，输出形式为整数序列：n,c1,e1,c2,e2,...,cn,en。其中n是多项式的项数，ci和ei分别是第i项的系数和指数，序列按指数降序排列。 3. 多项式a与多项式b相乘，建立多项式。 实验步骤： 1. 加法算法： a. 输入多项式P1和P2。 b. 创建一个空的和多项式P_sum。 c. 比较P1的第一项和P2的第一项的指数大小关系，将较大的项插入到P_sum中。 d. 依次比较P1和P2的下一项，并将较大的项插入到P_sum中。 e. 输出和多项式P_sum。 2. 乘法算法： a. 输入多项式P1和P2。 b. 创建一个空的积多项式P_product。 c. 用P1的第一项乘以P2的每一项，得到一个暂时的积多项式P_temp。 d. 依次用P1的每一项乘以P2，并将结果插入到P_temp中。 e. 搜索P_temp中的合适位置，将结果项插入到P_product中。 f. 输出积多项式P_product。 核心思想： 加法算法的核心思想是根据P1和P2项的指数大小关系，按照降序将它们插入和多项式中。 乘法算法的核心思想是先用P1的第一项乘以P2的每一项，得到一个暂时的积多项式。然后依次用P1的每一项乘以P2，并将结果插入到合适的位置。 时间复杂度分析： 加法算法的时间复杂度为O(n)，其中n为两个多项式中较大的项数。 乘法算法的时间复杂度为O(n^2)，其中n为两个多项式中较大的项数。 实验结果： 经过实验，本计算器能够正确执行多项式的加法和乘法运算，并以指定形式输出多项式。 实验总结： 本实验通过设计一个一元稀疏多项式简单计算器，实现了多项式的加法和乘法运算。加法算法按照指数降序将两个多项式相加，并输出和多项式。乘法算法先用第一项乘以第二个多项式的每一项，得到一个暂时的积多项式，然后将乘积插入到合适的位置，并输出积多项式。整个实验过程中，时间复杂度主要取决于多项式中较大的项数，加法算法的时间复杂度为O(n)，乘法算法的时间复杂度为O(n^2)。通过本次实验，加深了对于数据结构和算法的理解，对于原理性较强的数据结构的实现也有了一定的认识。在以后的学习和实践中，将会更加深入地探索多项式的相关算法和优化方法。