平衡二叉树与AVL树：高级数据结构解析

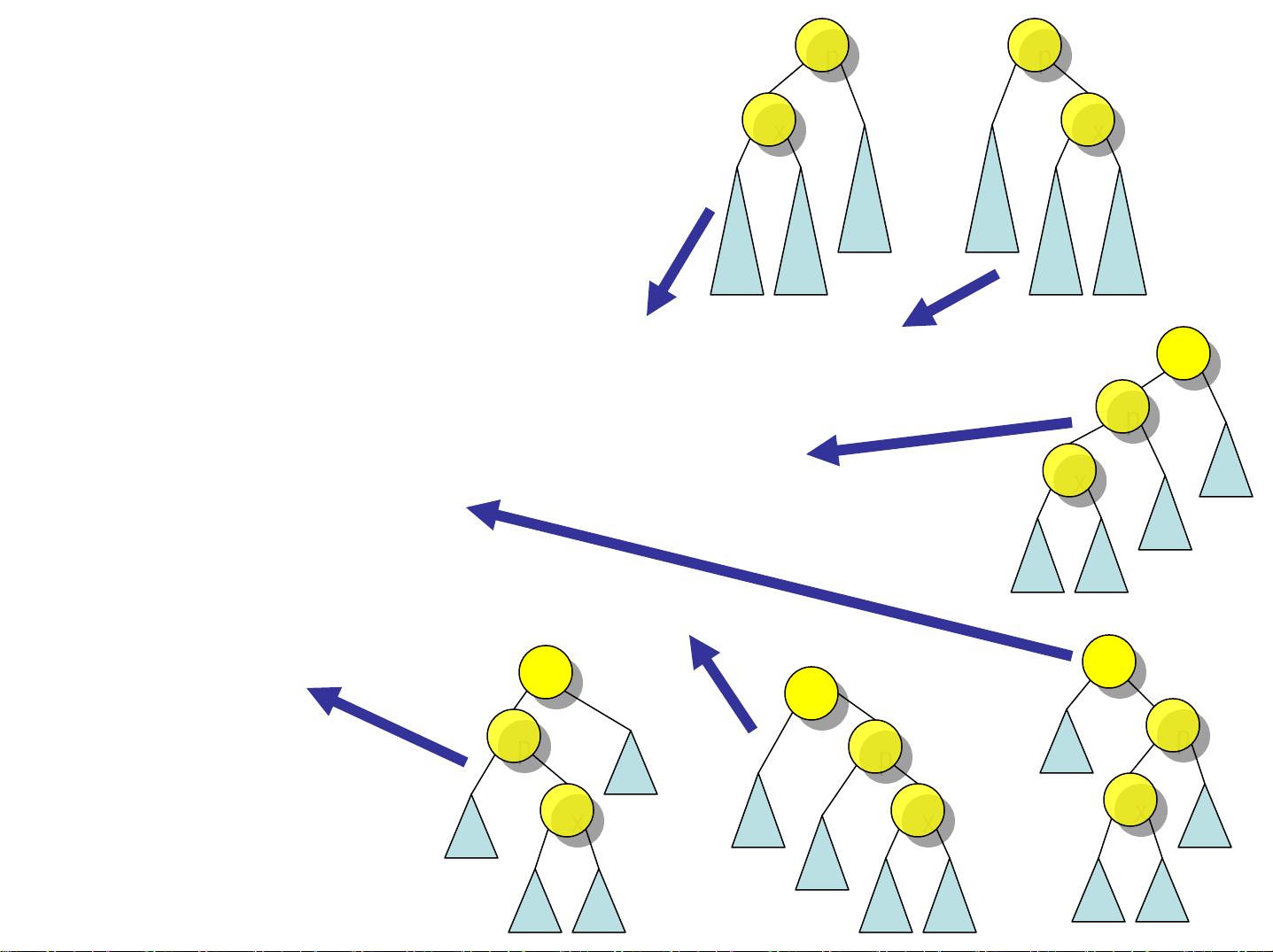
"《高级数据结构》由刘汝佳讲解，涵盖了高级数据结构的基础知识，适合想要在ACM竞赛领域深化理解的学员学习。课程主要涉及平衡二叉树、可并优先队列、线段树和树状数组基础，以及RMQ与LCA等重要概念。" 在计算机科学中，数据结构是算法设计和分析的关键，尤其对于解决复杂问题至关重要。本课程深入探讨了几个重要的高级数据结构，以提升算法效率。 一、平衡二叉树 平衡二叉树是一种特殊的二叉树，其目的是保持树的平衡，以优化查找、插入和删除等操作的时间复杂度。在基本的二叉搜索树（BST）中，左子树的所有节点小于根节点，右子树的所有节点大于根节点。然而，如果树不平衡，例如极度倾斜，这些操作可能退化为线性时间复杂度。理想的平衡状态是指树的高度为O(logn)，这样能保证操作的高效性。 二、AVL树 AVL树是最早的自平衡二叉搜索树之一。它通过限制每个节点的左右子树高度差不超过1来保持平衡。这意味着树的形状受到严格控制，确保了查找、插入和删除操作的时间复杂度都为O(logn)。AVL树的平衡调整通过旋转操作来实现，包括单旋转和双旋转，以恢复树的平衡状态。当插入新节点导致不平衡时，需要自底向上地向上找到第一个不平衡的节点，并进行相应的旋转调整。 三、可并优先队列 可并优先队列，又称二项堆或 Fibonacci堆，是一种能够高效地合并和删除最小元素的数据结构，常用于求解最短路径问题。在ACM竞赛中，可并优先队列常用于处理大量动态插入和删除请求的情况。 四、线段树和树状数组 线段树和树状数组是用于区间查询和更新的动态数据结构。线段树通过将一维数组分成多个重叠的子区间来实现，每个节点存储对应区间的值。树状数组（也称作 BIT，Binary Indexed Tree）利用位运算快速处理区间查询和更新，具有更紧凑的存储和更快的更新速度。 五、RMQ（Range Minimum Query）与LCA（Lowest Common Ancestor） RMQ问题是在一个数组或树中寻找指定范围内的最小值，而LCA问题是在树中找出两个节点的最近公共祖先。这两者在算法竞赛和数据结构应用中非常常见，特别是在动态维护区间信息时。 通过学习这些高级数据结构，不仅可以提高编程能力，还能够为参与ACM竞赛和解决实际问题提供强大的工具。理解并熟练掌握这些数据结构的原理和实现方法，是成为优秀算法工程师的关键步骤。