刘汝佳讲解：高级数据结构之平衡二叉树与AVL树

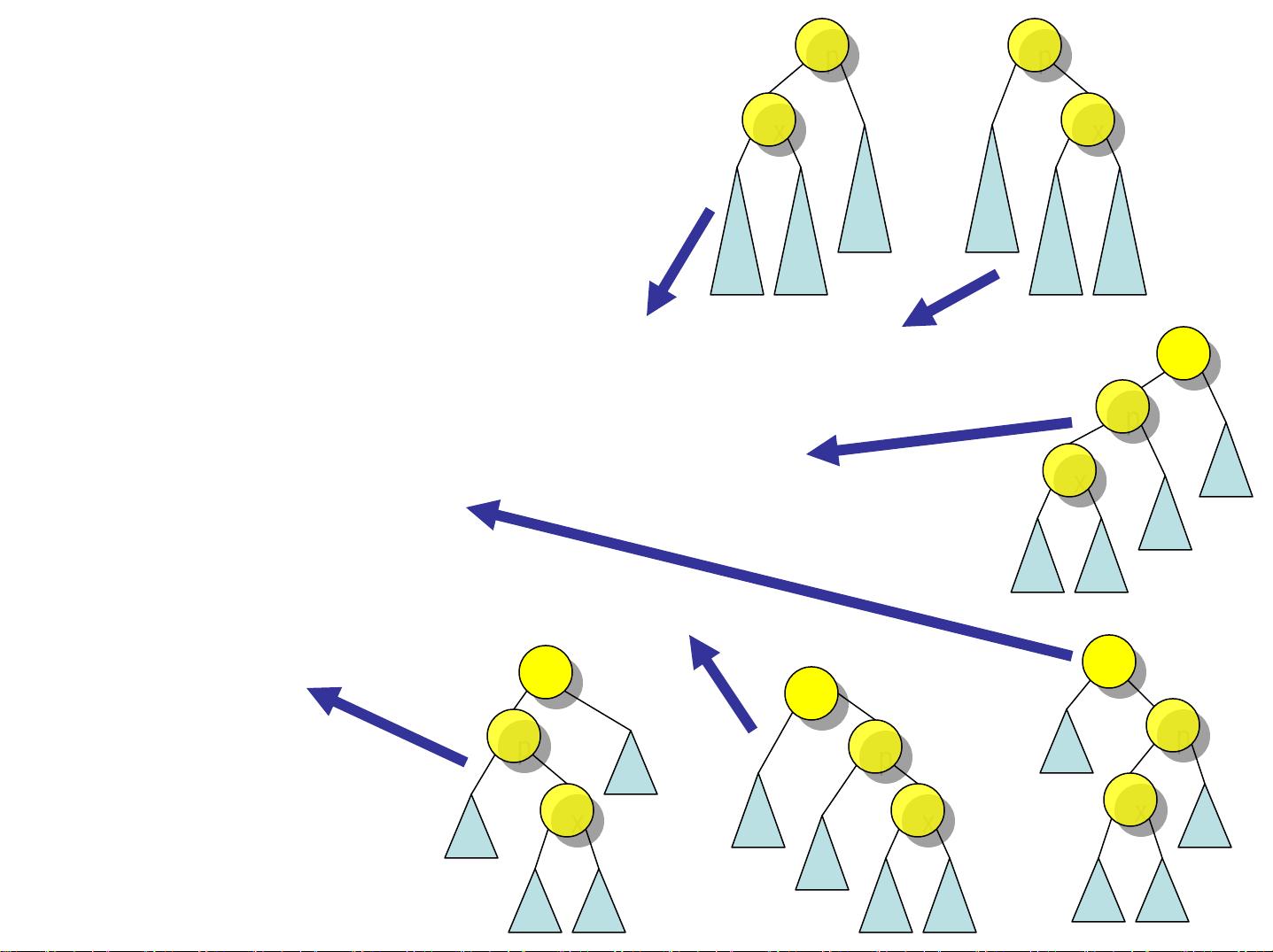
"刘汝佳 高级数据结构" 是一套专门讲解高级数据结构的教程，适合对ACM（国际大学生程序设计竞赛）感兴趣的学员学习。由ACM领域的大师刘汝佳主讲，课程涵盖了平衡二叉树、可并优先队列、线段树和树状数组基础、RMQ（Range Minimum Query，范围最小值查询）以及LCA（Lowest Common Ancestor，最近公共祖先）等重要主题。 一、平衡二叉树 平衡二叉树是一种特殊的二叉树，其左右子树的高度差不超过1，目的是确保在保持排序性质的同时，提高数据操作（如查找、插入和删除）的效率。基本的二叉搜索树（BST）在极端情况下可能会变得非常不平衡，导致操作性能下降。例如，如果树呈链式结构，高度会接近n，而不是理想的O(logn)。平衡二叉树通过维持相对平衡的形状，确保了高效的性能。 二、AVL树 AVL树是最早被提出的自平衡二叉搜索树，它的每个节点的左右子树高度差不超过1。AVL树的插入、删除和查找操作时间复杂度均为O(logn)。为了保持平衡，AVL树引入了旋转操作：单旋转和双旋转。当插入新节点导致某个节点的平衡因子（左右子树的高度差）超出限制时，需要进行相应的旋转来恢复平衡。单旋转分为右旋和左旋，而双旋转是先进行一次单旋转再进行另一次单旋转，用于处理更复杂的情况，如祖父节点与孙子节点不在同一垂直线上。 三、可并优先队列 可并优先队列是一种高效的数据结构，支持合并（merge）和找到最小元素（extractMin）等操作。在ACM竞赛中，它常用于处理动态集合的问题，如求最小生成树或解决区间问题。可并优先队列通常用堆来实现，如二叉堆，能够快速找到当前最小元素，并能合并两个优先队列。 四、线段树和树状数组基础 线段树是一种树形数据结构，用于高效地处理区间查询和区间更新问题。它可以将一个数组分成多个子区间，每个节点代表一个子区间的最大值、最小值或其他统计信息。树状数组，又称 BIT（Binary Indexed Tree），是另一种处理区间问题的方法，它通过数组表示，通过位运算快速完成区间累加和其他查询。 五、RMQ与LCA RMQ问题是在一个数组中查找给定区间内的最小值。最简单的解决方案是线性扫描，但在平衡树或树状数组等数据结构的支持下，可以实现O(logn)的复杂度。LCA问题则是在一棵树中找出两个指定节点的最近公共祖先。LCA算法有多种实现，如Morris遍历、Floyd判圈法和基于树链剖分的方法。 总结来说，"刘汝佳 高级数据结构"教程深入讲解了这些高级数据结构的原理、操作和应用，对于提升算法能力，特别是参与ACM竞赛的选手，具有很高的学习价值。通过学习，不仅能掌握数据结构的基础知识，还能理解如何在实际问题中选择和应用这些结构，以优化算法效率。