线性空间与数据挖掘：向量、变换与应用

"数据挖掘化功大法（11）——线性空间" 线性空间，又称向量空间，是线性代数中的基础概念，它将几何中的向量概念抽象化并与域（如实数域或复数域）相结合。在解析几何中，向量的引入简化了对几何问题的处理，而线性空间的概念则进一步深化了这种抽象。实系数多项式集合以及单变元实函数集合都可以构建成向量空间，分别在代数和泛函分析中有着重要的应用。 向量空间的定义包括两个基本运算：向量加法和标量乘法。向量加法具有结合律、交换律以及存在零向量和加法逆元的特性。标量乘法则遵循分配律、一致性和单位元的规则。在一些定义中，还要求向量空间对于向量加法和标量乘法是封闭的，即所有加法和标量乘法的结果仍在向量空间内。 基变换是线性空间中的重要概念，它涉及从一组基转换到另一组基的过程。过渡矩阵用于描述坐标的变化，同一个向量在不同基下的坐标表示可以通过这个矩阵进行转换。坐标变换是基变换的直观表现，它展示了向量在新旧基底下的坐标差异。 线性空间的子空间直和是指由一组子空间构成的集合，这些子空间两两相交且交集仅包含零向量。直和的子空间可以是正交的，这意味着它们在特定范数下互相垂直。 线性变换是保持向量加法和标量乘法不变的映射，它可以由方阵来描述。线性变换保留了直线和平行性，但可能改变长度、角度、面积和体积等几何特性。尽管如此，线性变换不会扭曲或弯曲坐标系，只会对其进行拉伸或压缩。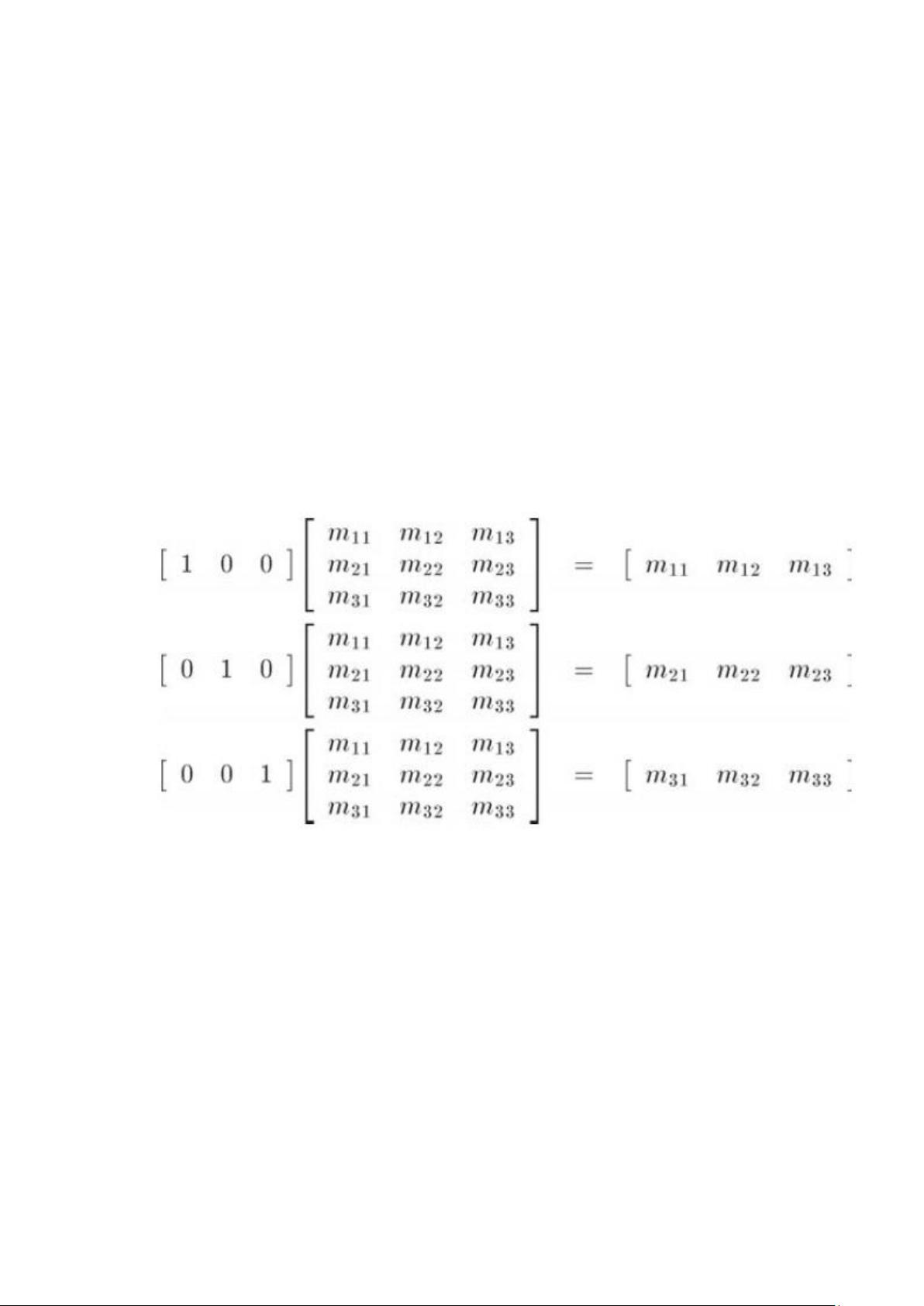 矩阵对向量的作用可以理解为对向量的位移的组合。任何向量都可以表示为基向量的线性组合，矩阵乘以向量的结果就是将原始向量在新的基向量下表示的形式。矩阵的每一列代表了一个基向量，而矩阵的行则对应了新基向量的坐标系数。 在数据挖掘中，线性空间和相关的概念，如向量、基变换和线性变换，被广泛应用。例如，特征向量可以看作是数据点在多维空间中的表示，通过降维技术如主成分分析（PCA）可以找到一个新的基，以减少特征维度的同时保留大部分信息。线性变换也可以用于构建分类器，如支持向量机（SVM），其中的核函数就是通过线性不可分数据的非线性映射来实现的。 线性空间及其相关理论为理解和处理复杂的数据提供了强大的工具，无论是在理论研究还是实际应用中都有着不可忽视的价值。