控制系统数学模型解析

"自动控制原理-胡寿松-第六版第二章ppt.ppt" 本文主要讨论的是自动控制原理中的一个重要概念——控制系统的数学模型。数学模型是描述系统动态特性和各变量间关系的数学表达式，它是控制系统进行定量分析的基础。在自动控制理论中，数学模型的建立对于理解和设计控制系统至关重要。 首先，数学模型的特点包括相似性、简化性和准确性。相似性是指尽管系统的物理性质可能不同，但它们可以拥有相同的数学模型，通过抽象的变量来表现。简化性强调在建模时要忽略次要因素，以简化模型，但必须确保结果的合理性。动态模型通常涉及变量的微分方程，用于分析系统的动态响应，而静态模型则关注在稳态条件下的代数关系。 数学模型的类型主要有三种：微分方程、传递函数和频率特性。微分方程是最基本的模型，它在时域中描述系统的行为，但直接求解可能较为复杂。传递函数是在复频域中对微分方程进行拉普拉斯变换的结果，适用于频域分析。频率特性则是通过不同的频域分析方法来评估系统性能。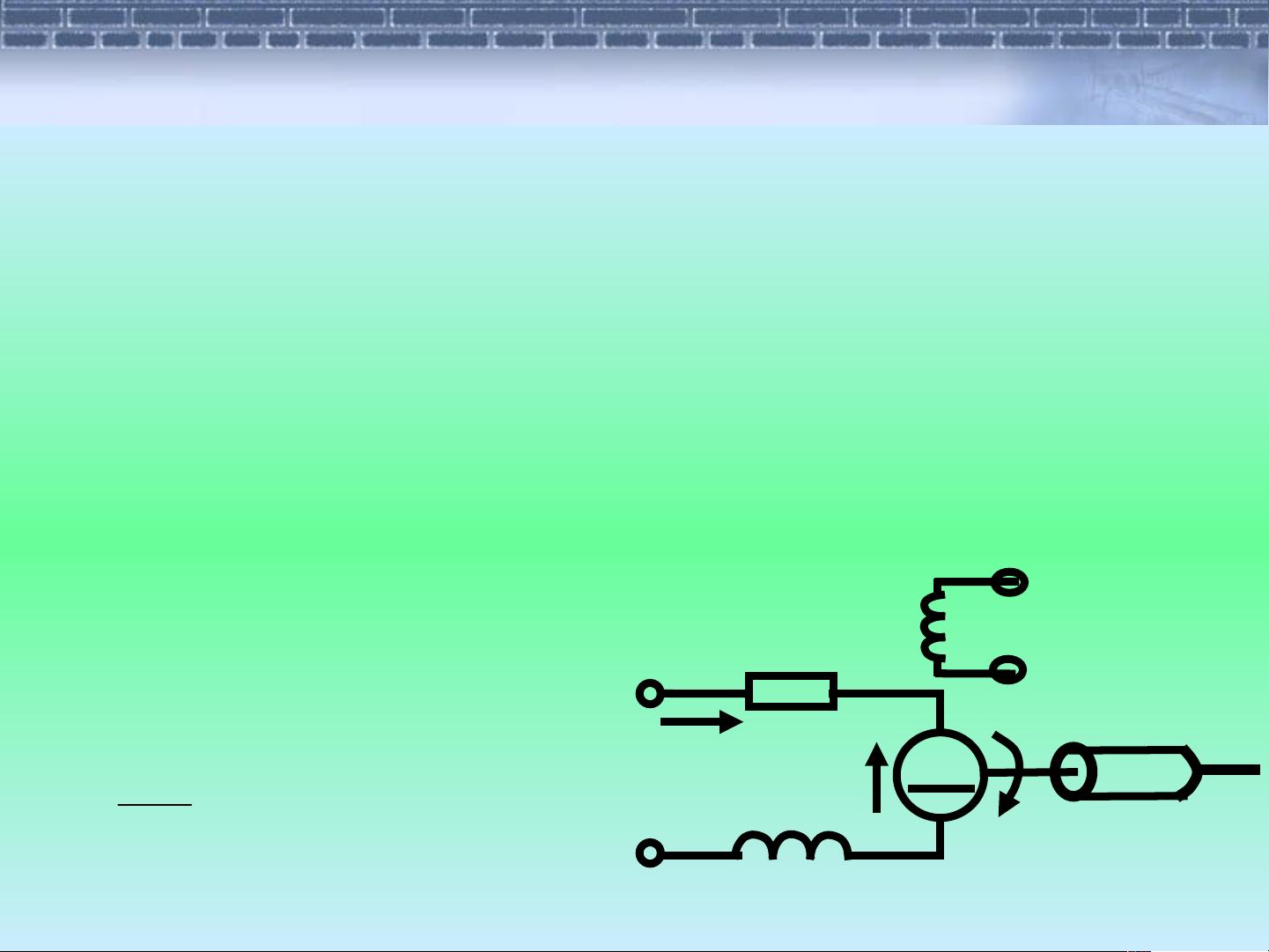 建立数学模型的方法主要包括分析法和实验法。分析法基于系统各部分的工作原理，根据物理定律列方程；实验法常用于处理“黑箱”问题，通过输入测试信号并记录输出，然后使用系统辨识技术确定模型。在建模过程中，应选择合适的分析方法，确定相应的数学模型，并进行必要的简化。 列写微分方程通常需要遵循一系列步骤：确定系统的输入、输出及内部变量，简化模型，依据基本物理定律列出原始方程，加入中间变量的辅助方程，联立方程并消除中间变量，最后将方程化为标准形式，即输入项在右边，输出项在左边，导数项按降阶排列，并将系数转换为物理意义明确的形式。 自动控制原理中的数学模型是理解和设计控制系统的关键，它涵盖了从微分方程到传递函数和频率特性的各种工具，以及如何通过分析法和实验法来建立和简化这些模型。这些理论和方法对于实际工程中的控制系统设计和优化具有重要意义。