PyTorch实现一维线性回归:理论与代码
41 浏览量
更新于2024-09-01
收藏 121KB PDF 举报
本文主要介绍了如何使用PyTorch构建一维线性回归模型,包括理论基础和实际代码实现。在理论部分,文章解释了线性回归的目标是找到最佳的直线来拟合数据,通过最小化均方误差损失函数来优化模型参数。在实践部分,通过创建一个简单的数据集并使用PyTorch的nn.Linear模块定义模型,展示了如何训练和应用模型。
一、一维线性回归模型理论基础
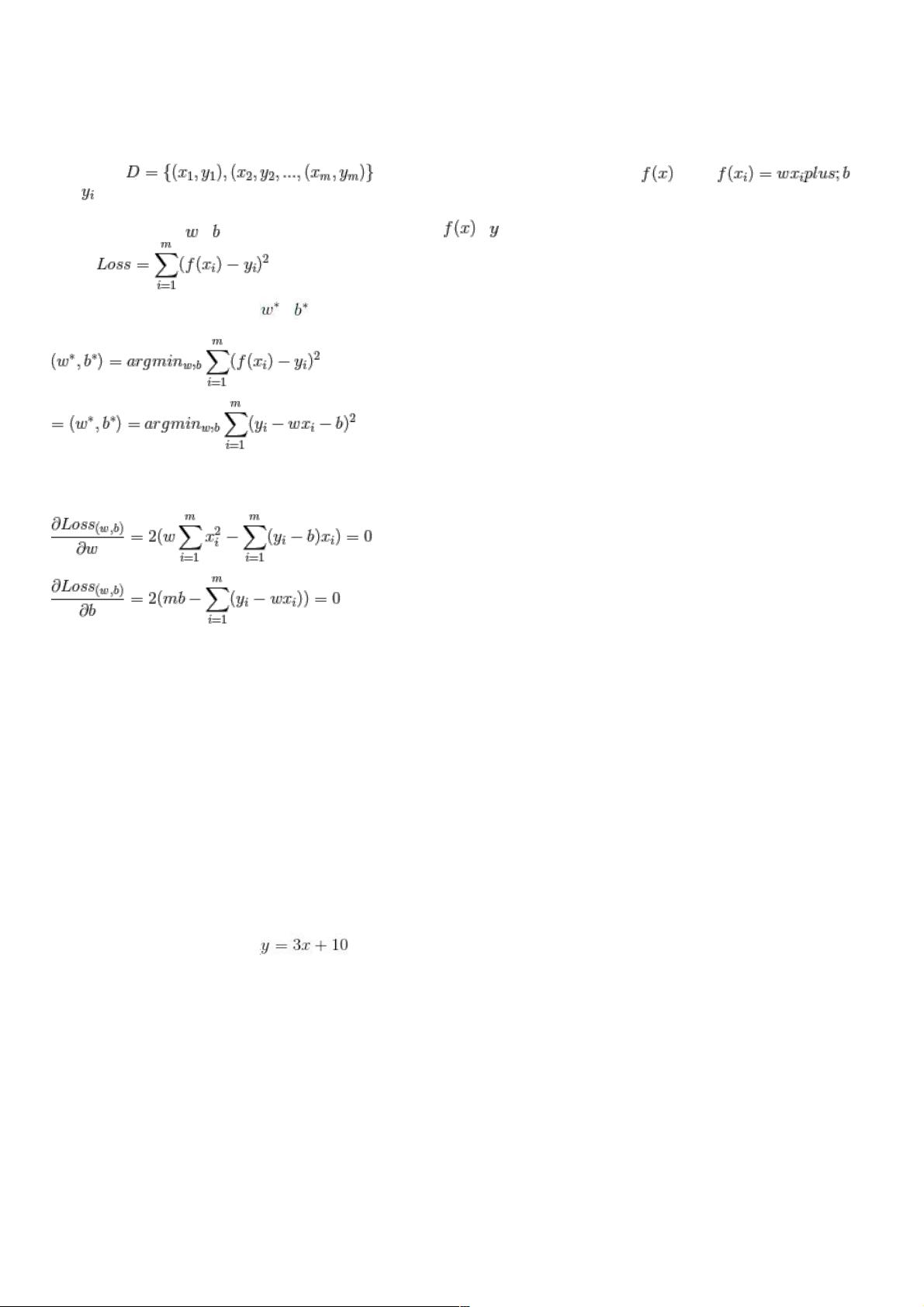
线性回归是一种基础的统计学方法,用于建立因变量和一个或多个自变量之间的线性关系。在一维线性回归中,模型假设数据可以用直线 y = wx + b 来表示,其中w是权重,b是偏置。为了找到最佳的w和b,我们需要一个衡量预测值与真实值之间差异的指标,这就是损失函数。在本例中,使用的是均方误差(Mean Squared Error, MSE),其计算公式为:
MSE = (1/n) * Σ[(y_pred - y_true)^2]
这里,n是样本数量,y_pred是模型预测值,y_true是真实值。取平方是为了确保误差始终为正,并且能更好地反映预测值远离真实值的程度。为了最小化MSE,我们需对w和b求偏导数,使其等于零,从而求得最小MSE时的参数值:
dw/dx = 0, db/dx = 0
解这两个方程可以得到w和b的最优值。
二、PyTorch实现一维线性回归模型
在PyTorch中,我们可以利用自动梯度机制和神经网络模块(nn.Module)轻松构建线性回归模型。首先,生成一个模拟数据集,如:
x = torch.linspace(-1, 1, 100) 扩展为二维张量,y = 3 * x + 10 + torch.rand(x.size()) 添加随机噪声。
然后,定义一个名为LinearRegression的类,继承自nn.Module。在__init__方法中,我们创建了一个nn.Linear层,输入和输出维度均为1。forward方法接收输入x并返回经过线性变换后的输出。
```python
class LinearRegression(nn.Module):
def __init__(self):
super(LinearRegression, self).__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
out = self.linear(x)
return out
```
如果GPU可用,模型会被移动到GPU上以加速计算:
```python
if torch.cuda.is_available():
model = LinearRegression().cuda()
```
接下来,我们需要定义优化器(optimizer)和损失函数(loss function),如SGD和MSELoss,然后进行训练迭代。每次迭代中,我们会更新模型参数以减小损失。
```python
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
criterion = nn.MSELoss()
for epoch in range(num_epochs): # 迭代次数
optimizer.zero_grad() # 清零梯度
outputs = model(x) # 模型预测
loss = criterion(outputs, y) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新参数
```
训练完成后,模型可用于预测新的x值对应的y值,评估模型性能可以通过计算训练集或测试集上的平均误差。
通过以上步骤,我们就用PyTorch成功实现了从数据生成、模型构建到训练的一维线性回归模型。这种模型简单易懂,是理解和掌握深度学习框架如PyTorch的绝佳起点。
2020-09-19 上传
2024-03-05 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
weixin_38601499
- 粉丝: 2
- 资源: 938
最新资源
- 正整数数组验证库:确保值符合正整数规则
- 系统移植工具集:镜像、工具链及其他必备软件包
- 掌握JavaScript加密技术:客户端加密核心要点
- AWS环境下Java应用的构建与优化指南
- Grav插件动态调整上传图像大小提高性能
- InversifyJS示例应用:演示OOP与依赖注入
- Laravel与Workerman构建PHP WebSocket即时通讯解决方案
- 前端开发利器:SPRjs快速粘合JavaScript文件脚本
- Windows平台RNNoise演示及编译方法说明
- GitHub Action实现站点自动化部署到网格环境
- Delphi实现磁盘容量检测与柱状图展示
- 亲测可用的简易微信抽奖小程序源码分享
- 如何利用JD抢单助手提升秒杀成功率
- 快速部署WordPress:使用Docker和generator-docker-wordpress
- 探索多功能计算器:日志记录与数据转换能力
- WearableSensing: 使用Java连接Zephyr Bioharness数据到服务器